As promised, let’s dive into the NFA’s class. To understand what’s an NFA, refer to the first post in this series called Regex engine in C# - the Regex Parser.
Last time we ended with the main Regex Engine class (RegexParser) which delegates to the NFA class the logic for constructing the NFA based on the parse tree we got on the last post.
The following is the NFA class:
// // Regular Expression Engine C# Sample Application // 2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite. // // UBM's Computer Engineering - 7th term [http://www.ubm.br/] // // This program sample was developed and turned in as a term paper for Lab. of // Compilers Construction. It was based on the source code provided by Eli Bendersky // [http://eli.thegreenplace.net/] and is provided "as is" without warranty. // // It makes use of C5 collections library (see reference at the end of this post.) // using System; using SCG = System.Collections.Generic; using C5; using state = System.Int32; using input = System.Char; namespace RegularExpressionEngine { /// <summary> /// Implements a non-deterministic finite automata /// </summary> class NFA { public state initial; public state final; private int size; // Inputs this NFA responds to public SortedArray<input> inputs; public input[][] transTable; /// <summary> /// Provides default values for epsilon and none /// </summary> public enum Constants { Epsilon = 'ε', None = '\0' } public NFA(NFA nfa) { initial = nfa.initial; final = nfa.final; size = nfa.size; inputs = nfa.inputs; transTable = nfa.transTable; } /// <summary> /// Constructed with the NFA size (amount of states), the initial state and the /// final state /// </summary> /// <param name="size_">Amount of states.</param> /// <param name="initial_">Initial state.</param> /// <param name="final_">Final state.</param> public NFA(int size_, state initial_, state final_) { initial = initial_; final = final_; size = size_; IsLegalState(initial); IsLegalState(final); inputs = new SortedArray<input>(); // Initializes transTable with an "empty graph", no transitions between its // states transTable = new input[size][]; for(int i = 0; i < size; ++i) transTable[i] = new input[size]; } public bool IsLegalState(state s) { // We have 'size' states, numbered 0 to size-1 if(s < 0 || s >= size) return false; return true; } /// <summary> /// Adds a transition between two states. /// </summary> /// <param name="from"></param> /// <param name="to"></param> /// <param name="in"></param> public void AddTrans(state from, state to, input @in) { IsLegalState(from); IsLegalState(to); transTable[from][to] = @in; if(@in != (char)Constants.Epsilon) inputs.Add(@in); } /// <summary> /// Fills states 0 up to other.size with other's states. /// </summary> /// <param name="other"></param> public void FillStates(NFA other) { for(state i = 0; i < other.size; ++i) for(state j = 0; j < other.size; ++j) transTable[i][j] = other.transTable[i][j]; SCG.IEnumerator<input> cE = other.inputs.GetEnumerator(); while(cE.MoveNext()) inputs.Add(cE.Current); } /// <summary> /// Renames all the NFA's states. For each nfa state: number += shift. /// Functionally, this doesn't affect the NFA, it only makes it larger and renames /// its states. /// </summary> /// <param name="shift"></param> public void ShiftStates(int shift) { int newSize = size + shift; if(shift < 1) return; // Creates a new, empty transition table (of the new size). input[][] newTransTable = new input[newSize][]; for(int i = 0; i < newSize; ++i) newTransTable[i] = new input[newSize]; // Copies all the transitions to the new table, at their new locations. for(state i = 0; i < size; ++i) for(state j = 0; j < size; ++j) newTransTable[i + shift][j + shift] = transTable[i][j]; // Updates the NFA members. size = newSize; initial += shift; final += shift; transTable = newTransTable; } /// <summary> /// Appends a new, empty state to the NFA. /// </summary> public void AppendEmptyState() { transTable = Resize(transTable, size + 1); size += 1; } private static input[][] Resize(input[][] transTable, int newSize) { input[][] newTransTable = new input[newSize][]; for(int i = 0; i < newSize; ++i) newTransTable[i] = new input[newSize]; for(int i = 0; i <= transTable.Length - 1; i++) for(int j = 0; j <= transTable[i].Length - 1; j++) { if(transTable[i][j] != '\0') newTransTable[i][j] = transTable[i][j]; } return newTransTable; } /// <summary> /// Returns a set of NFA states from which there is a transition on input symbol /// inp from some state s in states. /// </summary> /// <param name="states"></param> /// <param name="inp"></param> /// <returns></returns> public Set<state> Move(Set<state> states, input inp) { Set<state> result = new Set<state>(); // For each state in the set of states foreach(state state in states) { int i = 0; // For each transition from this state foreach(input input in transTable[state]) { // If the transition is on input inp, add it to the resulting set if(input == inp) { state u = Array.IndexOf(transTable[state], input, i); result.Add(u); } i = i + 1; } } return result; } /// <summary> /// Prints out the NFA. /// </summary> public void Show() { Console.WriteLine("This NFA has {0} states: 0 - {1}", size, size - 1); Console.WriteLine("The initial state is {0}", initial); Console.WriteLine("The final state is {0}\n", final); for(state from = 0; from < size; ++from) { for(state to = 0; to < size; ++to) { input @in = transTable[from][to]; if(@in != (char)Constants.None) { Console.Write("Transition from {0} to {1} on input ", from, to); if(@in == (char)Constants.Epsilon) Console.Write("Epsilon\n"); else Console.Write("{0}\n", @in); } } } Console.Write("\n\n"); } /// <summary> /// /// </summary> /// <param name="tree"></param> /// <returns></returns> public static NFA TreeToNFA(ParseTree tree) { switch (tree.type) { case ParseTree.NodeType.Chr: return BuildNFABasic(tree.data.Value); case ParseTree.NodeType.Alter: return BuildNFAAlter(TreeToNFA(tree.left), TreeToNFA(tree.right)); case ParseTree.NodeType.Concat: return BuildNFAConcat(TreeToNFA(tree.left), TreeToNFA(tree.right)); case ParseTree.NodeType.Star: return BuildNFAStar(TreeToNFA(tree.left)); case ParseTree.NodeType.Question: return BuildNFAAlter(TreeToNFA(tree.left), BuildNFABasic((char)Constants.Epsilon)); default: return null; } } ///////////////////////////////////////////////////////////////// // // NFA building functions // // Using Thompson Construction, build NFAs from basic inputs or // compositions of other NFAs. // /// <summary> /// Builds a basic, single input NFA /// </summary> /// <param name="in"></param> /// <returns></returns> public static NFA BuildNFABasic(input @in) { NFA basic = new NFA(2, 0, 1); basic.AddTrans(0, 1, @in); return basic; } /// <summary> /// Builds an alternation of nfa1 and nfa2 (nfa1|nfa2) /// </summary> /// <param name="nfa1"></param> /// <param name="nfa2"></param> /// <returns></returns> public static NFA BuildNFAAlter(NFA nfa1, NFA nfa2) { // How this is done: the new nfa must contain all the states in // nfa1 and nfa2, plus a new initial and final states. // First will come the new initial state, then nfa1's states, then // nfa2's states, then the new final state // make room for the new initial state nfa1.ShiftStates(1); // make room for nfa1 nfa2.ShiftStates(nfa1.size); // create a new nfa and initialize it with (the shifted) nfa2 NFA newNFA = new NFA(nfa2); // nfa1's states take their places in new_nfa newNFA.FillStates(nfa1); // Set new initial state and the transitions from it newNFA.AddTrans(0, nfa1.initial, (char)Constants.Epsilon); newNFA.AddTrans(0, nfa2.initial, (char)Constants.Epsilon); newNFA.initial = 0; // Make up space for the new final state newNFA.AppendEmptyState(); // Set new final state newNFA.final = newNFA.size - 1; newNFA.AddTrans(nfa1.final, newNFA.final, (char)Constants.Epsilon); newNFA.AddTrans(nfa2.final, newNFA.final, (char)Constants.Epsilon); return newNFA; } /// <summary> /// Builds an alternation of nfa1 and nfa2 (nfa1|nfa2) /// </summary> /// <param name="nfa1"></param> /// <param name="nfa2"></param> /// <returns></returns> public static NFA BuildNFAConcat(NFA nfa1, NFA nfa2) { // How this is done: First will come nfa1, then nfa2 (its initial state replaced // with nfa1's final state) nfa2.ShiftStates(nfa1.size - 1); // Creates a new NFA and initialize it with (the shifted) nfa2 NFA newNFA = new NFA(nfa2); // nfa1's states take their places in newNFA // note: nfa1's final state overwrites nfa2's initial state, // thus we get the desired merge automatically (the transition // from nfa2's initial state now transits from nfa1's final state) newNFA.FillStates(nfa1); // Sets the new initial state (the final state stays nfa2's final state, // and was already copied) newNFA.initial = nfa1.initial; return newNFA; } /// <summary> /// Builds a star (kleene closure) of nfa (nfa*) /// How this is done: First will come the new initial state, then NFA, then the new final state /// </summary> /// <param name="nfa"></param> /// <returns></returns> public static NFA BuildNFAStar(NFA nfa) { // Makes room for the new initial state nfa.ShiftStates(1); // Makes room for the new final state nfa.AppendEmptyState(); // Adds new transitions nfa.AddTrans(nfa.final, nfa.initial, (char)Constants.Epsilon); nfa.AddTrans(0, nfa.initial, (char)Constants.Epsilon); nfa.AddTrans(nfa.final, nfa.size - 1, (char)Constants.Epsilon); nfa.AddTrans(0, nfa.size - 1, (char)Constants.Epsilon); nfa.initial = 0; nfa.final = nfa.size - 1; return nfa; } } }
We pass the parse tree (see last post) to a function responsible for converting the parse tree to an NFA.
private NFA TreeToNFA(ParseTree tree) { switch(tree.type) { case ParseTree.NodeType.Chr: return BuildNFABasic(tree.data.Value); case ParseTree.NodeType.Alter: return BuildNFAAlter(TreeToNFA(tree.left), TreeToNFA(tree.right)); case ParseTree.NodeType.Concat: return BuildNFAConcat(TreeToNFA(tree.left), TreeToNFA(tree.right)); case ParseTree.NodeType.Star: return BuildNFAStar(TreeToNFA(tree.left)); case ParseTree.NodeType.Question: return BuildNFAAlter(TreeToNFA(tree.left), BuildNFABasic((char)Constants.Epsilon)); default: return null; } }
The TreeToNFA function delegates to the building functions that employ Thompson Construction to build the NFA from basic inputs or compositions of other NFAs.
TreeToNFA is recursive! It calls itself, that is, the calls are put into the stack. Debug the code to see how it works.
The building functions are well documented. Take a look at the comments in the code above.
While debugging the code we get the following variables’ structure:
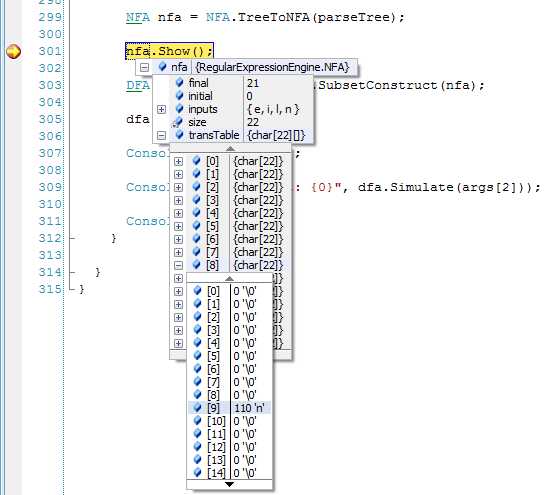
Figure 1 - Variables' structure while in debugging mode
From the above picture we see that there’s a transition from state 8 to state 9 with the input symbol ‘n’.
The NFA’s Show function will only output something if the transition’s value present in the transTable variable is different from 0 ‘\0’, that is, if there’s indeed a transition from one state to another.
So, for the regex (l|e)*n?(i|e)el* we get the following transition table:
| This NFA has 22 states: 0 - 21
The initial state is 0 The final state is 21 |
| Transition from 0 to 1 on input Epsilon |
| Transition from 0 to 7 on input Epsilon |
| Transition from 1 to 2 on input Epsilon |
| Transition from 1 to 4 on input Epsilon |
| Transition from 2 to 3 on input l |
| Transition from 3 to 6 on input Epsilon |
| Transition from 4 to 5 on input e |
| Transition from 5 to 6 on input Epsilon |
| Transition from 6 to 1 on input Epsilon |
| Transition from 6 to 7 on input Epsilon |
| Transition from 7 to 8 on input Epsilon |
| Transition from 7 to 10 on input Epsilon |
| Transition from 8 to 9 on input n |
| Transition from 9 to 12 on input Epsilon |
| Transition from 10 to 11 on input Epsilon |
| Transition from 11 to 12 on input Epsilon |
| Transition from 12 to 13 on input Epsilon |
| Transition from 12 to 15 on input Epsilon |
| Transition from 13 to 14 on input i |
| Transition from 14 to 17 on input Epsilon |
| Transition from 15 to 16 on input e |
| Transition from 16 to 17 on input Epsilon |
| Transition from 17 to 18 on input e |
| Transition from 18 to 19 on input Epsilon |
| Transition from 18 to 21 on input Epsilon |
| Transition from 19 to 20 on input l |
| Transition from 20 to 19 on input Epsilon |
| Transition from 20 to 21 on input Epsilon |
This is the NFA’s graph representation:

Figure 3 - NFA’s graph representation for the regex (l|e)*n?(i|e)el*
As you see, some states have an eps-transition – eps or epsilon (ε) that represents "nothing" or "no input". This is absolutely valid in an NFA.
Next time we’ll dive into the DFA class that uses a subset machine to construct a DFA based on an NFA.
See you there!
Updated on 5/12/2009 09:54:00 PM
As I finished writing the posts, here goes the list that points to them:
Regular Expression Engine in C# (the Story)
Regex engine in C# - the Regex Parser
Regex engine in C# - the DFA
Regex engine in C# - matching strings
Source code: https://github.com/leniel/RegexEngine
References
[1] Kokholm, Niels; Sestoft, Peter. The C5 Generic Collection Library for C# and CLI. Available at <http://www.itu.dk/research/c5/>. Accessed on May 2, 2008.




