To close this series of posts, today I’m going to match some input strings using the regex (l|e)*n?(i|e)el* that we’ve been using since the beginning.

To match the strings I’ll make use of the DFA we constructed in the last post titled Regex engine in C# - the DFA.

These are the 20 strings I’ll be matching:

eee, eeeil, eel, ennil, ie, leie, lele, leleel, lelel, lelenil, leliel, leniel, llnel, ln, lnel, lniel, nelll, niel, nil and nll.

In the DFA class we have a method called Simulate which I show bellow:

public string Simulate(string @in)
{
  state currentState = start;

  CharEnumerator i = @in.GetEnumerator();

  while(i.MoveNext())
  {
    KeyValuePair<state, input> transition = new KeyValuePair<state, input>(currentState, i.Current);

    if(!transTable.ContainsKey(transition))
      return "Rejected";

    currentState = transTable[transition];
  }

  if(final.Contains(currentState))
    return "Accepted";
  else
    return "Rejected";
}

The Simulate method takes as input a string to be matched and returns a string that signalizes success or failing when matching such a string.

To test it I’ll match the string “leniel” which by the way is my own name. :-)

So, what the Simulate method do?

It starts by assigning the start state 0 to the variable currentState.

Next we get a charEnumerator that is used in the while block to move letter by letter (input symbol by input symbol) till we get to the end of the string.

We declare a KeyValuePair<state, input> designated transition that has as the key the currentState and as the value the current input symbol we’re simulating.

We check to see if the DFA’s transition table contains such a transition, that is, if there’s a valid path from that state with that input symbol to another state. If it doesn’t, we reject the string we’re matching, otherwise we make the currentState variable receive the next state, that is, the state appointed by the transition we’ve just checked.

The process inside the while block goes on until we reach the last input symbol taken from the string we’re matching, in this case, the last “l” letter.

After getting out of the while block we make a final check to see if the state we achieved is part of the DFA’s set of final states. If it is, we accept the string, otherwise, we reject it.

This is an x-ray from the variables’ value when in the first iteration of the while block:

As you can see in the transition table, from start state (currentState) “0” with the fist input symbol “l” we can go to state “3”.

The following table shows the result obtained while testing the strings mentioned above:

Accepted	Rejected
eee	eeeil
eel	ennil
ie	lele
leie	lelel
leleel	lelenil
leliel	llnel
leniel	ln
lniel	lnel
niel	nelll
	nil
	nll

To make sure it’s correct, debug each one of these strings visually looking at the DFA’s graph representation shown below. Starting at state 0 we must end in one of the final states {7, 8, 9, 10}.

The Regex Engine executable
The Regex Engine presented in this series of posts is a C# Console Application. As such it was written in a way that its command line arguments must be entered in the following form:

RegularExpressionEngine "(l|e)*n?(i|e)el*" leniel

Where:

RegularExpressionEngine ->  the name of the executable .exe file (the program itself)

"(l|e)*n?(i|e)el*" –> between the double quotes we pass the regex

leniel –> the string we want to match in the regex

Using Microsoft Visual Studio C# 2008 we can set the command line arguments using the Debug properties page of the project like the following picture:

To get to the Debug page, right click in the solution inside Solution Explorer as shown in the following picture:

After setting the command line arguments, hit F5 and you’re ready to go.

The Regex Engine source code
You can get the complete code (Microsoft Visual C# 2008 Console application) and executable at:

http://leniel.googlepages.com/RegularExpressionEngine.rar

To try out the code you can use the free Microsoft Visual C# 2008 Express Edition that you can get at: http://www.microsoft.com/express/vcsharp

Updated on 5/12/2009 10:06:00 PM

As I finished writing the posts, here goes the list that points to them:

Regular Expression Engine in C# (the Story)
Regex engine in C# - the Regex Parser
Regex engine in C# - the NFA
Regex engine in C# - the DFA

Source code: https://github.com/leniel/RegexEngine

References
The following links can help you when dealing with regexes:

Regular-Expressions.info - Regex Tutorial, Examples and Reference - Regex Patterns
http://www.regular-expressions.info

Regular Expression Library (great site with lots of regexes and an excellent regex tester)
http://regexlib.com/Default.aspx
http://regexlib.com/RETester.aspx

This time, we’ll take a look at the DFA’s class and its helper class called SubsetMachine.

To understand what’s a DFA, refer to the first post in this series called Regex engine in C# - the Regex Parser.

In the Regex engine in C# - the NFA post we ended with an NFA.

Now we’re going to build a DFA based on such NFA.

Remember that the main difference between a DFA and an NFA is that a DFA doesn’t have epsilon (ε) transitions that represent "nothing" or "no input" between states.

As described in the section DFA versus NFA in the introduction of this series of posts, it may be shown that a DFA is equivalent to an NFA, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction or subset construction.

So, let’s get our hands dirty with some code.

Below I present the DFA class:

//
//  Regular Expression Engine C# Sample Application
//  2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
//  UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//  
//  This program sample was developed and turned in as a term paper for Lab. of
//  Compilers Construction. It was based on the source code provided by Eli Bendersky
//  [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//

using System;
using SCG = System.Collections.Generic;
using C5;

using state = System.Int32;
using input = System.Char;

namespace RegularExpressionEngine
{
  /// <summary>
  /// Implements a deterministic finite automata (DFA)
  /// </summary>
  class DFA
  {
    // Start state
    public state start;
    // Set of final states
    public Set<state> final;
    // Transition table
    public SCG.SortedList<KeyValuePair<state, input>, state> transTable;

    public DFA()
    {
      final = new Set<state>();

      transTable = new SCG.SortedList<KeyValuePair<state, input>, state>(new Comparer());
    }

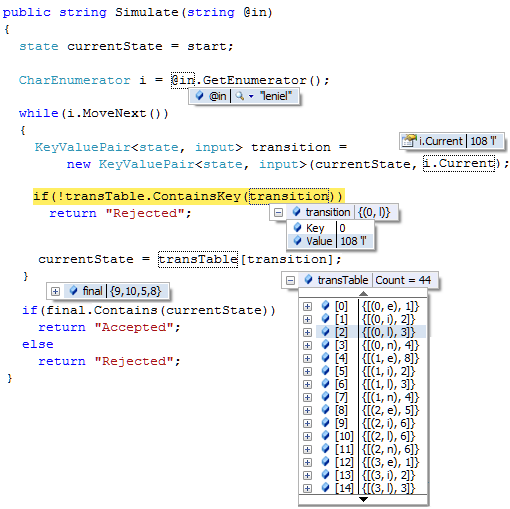
    public string Simulate(string @in)
    {
      state curState = start;

      CharEnumerator i = @in.GetEnumerator();

      while(i.MoveNext())
      {
        KeyValuePair<state, input> transition = new KeyValuePair<state, input>(curState, i.Current);

        if(!transTable.ContainsKey(transition))
          return "Rejected";

        curState = transTable[transition];
      }

      if(final.Contains(curState))
        return "Accepted";
      else
        return "Rejected";
    }

    public void Show()
    {
      Console.Write("DFA start state: {0}\n", start);
      Console.Write("DFA final state(s): ");

      SCG.IEnumerator<state> iE = final.GetEnumerator();

      while(iE.MoveNext())
        Console.Write(iE.Current + " ");

      Console.Write("\n\n");

      foreach(SCG.KeyValuePair<KeyValuePair<state, input>, state> kvp in transTable)
        Console.Write("Trans[{0}, {1}] = {2}\n", kvp.Key.Key, kvp.Key.Value, kvp.Value);
    }
  }

  /// <summary>
  /// Implements a comparer that suits the transTable SordedList
  /// </summary>
  public class Comparer : SCG.IComparer<KeyValuePair<state, input>>
  {
    public int Compare(KeyValuePair<state, input> transition1, KeyValuePair<state, input> transition2)
    {
      if(transition1.Key == transition2.Key)
        return transition1.Value.CompareTo(transition2.Value);
      else
        return transition1.Key.CompareTo(transition2.Key);
    }
  }

}

As you see, a DFA has 3 variables: a start state, a set of final states and a transition table that maps transitions between states.

Below I present the SubsetMachine class that is responsible for the hard work of extracting an equivalent DFA from a given NFA:

//
//  Regular Expression Engine C# Sample Application
//  2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
//  UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//  
//  This program sample was developed and turned in as a term paper for Lab. of
//  Compilers Construction. It was based on the source code provided by Eli Bendersky
//  [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//

using System;
using SCG = System.Collections.Generic;
using C5;

using state = System.Int32;
using input = System.Char;

namespace RegularExpressionEngine
{
  class SubsetMachine
  {
    private static int num = 0;

    /// <summary>
    /// Subset machine that employs the powerset construction or subset construction algorithm.
    /// It creates a DFA that recognizes the same language as the given NFA.
    /// </summary>
    public static DFA SubsetConstruct(NFA nfa)
    {
      DFA dfa = new DFA();

      // Sets of NFA states which is represented by some DFA state
      Set<Set<state>> markedStates = new Set<Set<state>>();
      Set<Set<state>> unmarkedStates = new Set<Set<state>>();

      // Gives a number to each state in the DFA
      HashDictionary<Set<state>, state> dfaStateNum = new HashDictionary<Set<state>, state>();

      Set<state> nfaInitial = new Set<state>();
      nfaInitial.Add(nfa.initial);

      // Initially, EpsilonClosure(nfa.initial) is the only state in the DFAs states and it's unmarked.
      Set<state> first = EpsilonClosure(nfa, nfaInitial);
      unmarkedStates.Add(first);

      // The initial dfa state
      state dfaInitial = GenNewState();
      dfaStateNum[first] = dfaInitial;
      dfa.start = dfaInitial;

      while(unmarkedStates.Count != 0)
      {
        // Takes out one unmarked state and posteriorly mark it.
        Set<state> aState = unmarkedStates.Choose();

        // Removes from the unmarked set.
        unmarkedStates.Remove(aState);

        // Inserts into the marked set.
        markedStates.Add(aState);

        // If this state contains the NFA's final state, add it to the DFA's set of
        // final states.
        if(aState.Contains(nfa.final))
          dfa.final.Add(dfaStateNum[aState]);

        SCG.IEnumerator<input> iE = nfa.inputs.GetEnumerator();

        // For each input symbol the nfa knows...
        while(iE.MoveNext())
        {
          // Next state
          Set<state> next = EpsilonClosure(nfa, nfa.Move(aState, iE.Current));

          // If we haven't examined this state before, add it to the unmarkedStates and make up a new number for it.
          if(!unmarkedStates.Contains(next) && !markedStates.Contains(next))
          {
            unmarkedStates.Add(next);
            dfaStateNum.Add(next, GenNewState());
          }

          KeyValuePair<state, input> transition = new KeyValuePair<state, input>();
          transition.Key = dfaStateNum[aState];
          transition.Value = iE.Current;

          dfa.transTable[transition] = dfaStateNum[next];
        }
      }

      return dfa;
    }

    /// <summary>
    /// Builds the Epsilon closure of states for the given NFA 
    /// </summary>
    /// <param name="nfa"></param>
    /// <param name="states"></param>
    /// <returns></returns>
    static Set<state> EpsilonClosure(NFA nfa, Set<state> states)
    {
      // Push all states onto a stack
      SCG.Stack<state> uncheckedStack = new SCG.Stack<state>(states);

      // Initialize EpsilonClosure(states) to states
      Set<state> epsilonClosure = states;

      while(uncheckedStack.Count != 0)
      {
        // Pop state t, the top element, off the stack
        state t = uncheckedStack.Pop();

        int i = 0;

        // For each state u with an edge from t to u labeled Epsilon
        foreach(input input in nfa.transTable[t])
        {
          if(input == (char)NFA.Constants.Epsilon)
          {
            state u = Array.IndexOf(nfa.transTable[t], input, i);

            // If u is not already in epsilonClosure, add it and push it onto stack
            if(!epsilonClosure.Contains(u))
            {
              epsilonClosure.Add(u);
              uncheckedStack.Push(u);
            }
          }

          i = i + 1;
        }
      }

      return epsilonClosure;
    }

    /// <summary>
    /// Creates unique state numbers for DFA states
    /// </summary>
    /// <returns></returns>
    private static state GenNewState()
    {
      return num++;
    }

  }
}

In the first post of this series we see the following line of code:

DFA dfa = SubsetMachine.SubsetConstruct(nfa);

The SubsetConstruct method from the SubsetMachine class receives as input an NFA and returns a DFA.

Inside the SubsetConstruct method we firstly instantiate a new DFA object and then we create two variables markedStates and unmarkedStates that are sets of NFA states which represent a DFA state.

// Sets of NFA states which is represented by some DFA state
Set<Set<state>> markedStates = new Set<Set<state>>();
Set<Set<state>> unmarkedStates = new Set<Set<state>>();

From this we see that a DFA state can represent a set of NFA states. Take a look at the introductory post and see Figure 2. It shows two DFA states that represent sets of NFA states, in this particular case the DFA final states represent the NFA states {s2, s3} and {s5, s6}.

The HashDictionary helps us to give a name (to number) each DFA state.

// Gives a number to each state in the DFA
HashDictionary<Set<state>, state> dfaStateNum = new HashDictionary<Set<state>, state>();

We declare a variable called nfaInitial that is a set of states. It receives the initial NFA state:

Set<state> nfaInitial = new Set<state>();
nfaInitial.Add(nfa.initial);

We’ll start using the EpsilonClosure function. 

// Initially, EpsilonClosure(nfa.initial) is the only state in the DFAs states and it's unmarked.
Set<state> first = EpsilonClosure(nfa, nfaInitial);

The EpsilonClosure function receives as parameters the NFA and its initial state and returns a set of states. Take a look at the method signature:

static Set<state> EpsilonClosure(NFA nfa, Set<state> states)

So, what does it do? You may ask. To answer this question let’s debug this first method call:

From the NFA transition table presented in Figure 2 and from the transition graph presented in Figure 3 in the second post of this series we can see how many transitions are represented by eps transitions.

The first time we enter into this function we’ll get as a return value a set of states that contains all the states that are reachable with an eps transition from the start state 0.

Figure 1 - States reachable by an eps transition from start state 0.

For the sake of comparison I’ll show the NFA’s graph representation for the regex (l|e)*n?(i|e)el* that we’re studying since the beginning of this series.

Figure 2 - NFA’s graph representation for the regex (l|e)*n?(i|e)el*

If you pay close attention you’ll see that the order the regex parser found the states is the order we visually debug the code looking at the graph above.

With such states found we move next adding this DFA state into the variable unmarkedStates.

We then use a function called GetNewState that is responsible for generating a number that uniquely identifies each state of the DFA:

// The initial dfa state
state dfaInitial = GenNewState();

When we pass to the next line of code we add to the dfaStateNum dictionary a key that is the set of states returned by the EpsilonClosure function and a value that is the name of the initial state of the DFA.

dfaStateNum[first] = dfaInitial;

We make the initial state of the DFA be the dfaInitial value we just got. 

dfa.start = dfaInitial;

Next we enter in the first while keyword. In this while we basically extract one of the unmarkedStates and add the same to the markedStates set. This has the meaning of telling that we already checked such state.

// Takes out one unmarked state and posteriorly mark it.
Set<state> aState = unmarkedStates.Choose();

// Removes from the unmarked set.
unmarkedStates.Remove(aState);

// Inserts into the marked set.
markedStates.Add(aState);

In the next line of code (one of the most interesting parts of the whole code) we check to see if this current DFA state (remember that it is a set of states) we’re on contains the NFA final state, if it holds true, we add it to the DFA’s set of final states:

// If this state contains the NFA's final state, add it to the DFA's set of final states.
if(aState.Contains(nfa.final))
  dfa.final.Add(dfaStateNum[aState]);

Now it’s time to check against the NFA’s input symbols. To accomplish this we declare an enumerator of type state that does the job of moving through each of the input symbols in the next while code block:

SCG.IEnumerator<input> iE = nfa.inputs.GetEnumerator();

// For each input symbol the nfa knows...
while(iE.MoveNext())
{ . . .

Now it’s time to create the next DFA state. We do this by declaring a new set of states and we call the EpsilonClosure function again to fill this state, but this time we pass the EpsilonClosure function a different second parameter.

// Next state
Set<state> next = EpsilonClosure(nfa, nfa.Move(aState, iE.Current));

Let’s go deeper to take a look at this second parameter.

As you see we call the function Move that is part of the NFA class. This function receives as parameters a set of states and an input symbol to be checked against. It returns a set of states.

What the move function does is: foreach state in the set of states passed as the first parameter we check each transition present in the NFA’s transition table from this state to another state with the input symbol passed as the second parameter.

So, the first time we pass we get the following output from the Move function:

Figure 3 - Result from the NFA’s Move function the 1st time it’s called

If we look at Figure 2  we can assert that from the states present in the first state of the DFA (see Figure 1) we can move to states {5, 16} with the first NFA input that is equal to ‘e’.

With the above result taken from the Move function we’re ready to go the EpsilonClosure function for the second time to create the 2nd DFA state in the SubsetMachine class. This second time we get the following result from EpsilonClosure function:

Figure 4 - Result from the EpsilonClosure function the 2nd time it’s called

Now, if you pay close attention, we can assert that starting at the states {5, 16} we can move with an eps-transition to the states shown above. Remember that the states we pass to the EpsilonClosure function are themselves included in the result returned by the function.

Now that we have created the 2nd DFA state we check to see if it wasn’t examined yet and if it holds true we add it to the unmarkedStates variable and give a new name to this state numbering it with the GenNewState function.

// If we haven't examined this state before, add it to the unmarkedStates and make up a new number for it.
if(!unmarkedStates.Contains(next) && !markedStates.Contains(next))
{
  unmarkedStates.Add(next);
  dfaStateNum.Add(next, GenNewState());
}

Now the best part of it. :)

We create a new transition that has as key the number of the DFA state we’re checking and as the value the current input symbol we’re after.

KeyValuePair<state, input> transition = new KeyValuePair<state, input>();
transition.Key = dfaStateNum[aState];
transition.Value = iE.Current;

We then add this transition to the DFA’s transition table:

Figure 5 - DFA’s transition table

This has the following meaning: from state 0 with input ‘e’ go to state 1!

These are the subsequent values we get for the first unmarkedState we’re checking:

With input ‘i’ we can go to state { 14 } from which with an eps transition we can go to state { 17 }.

With input ‘l’ we can go to state { 3 } from which with an eps transition we can go to states { 4, 13, 8, 3, 12, 7, 2, 11, 6, 1, 15, 10 }.

With input ‘n’ we can go to state { 9 } from which with an eps transition we can go to states { 12, 9, 13, 15 }.

A point that deserves consideration is that each time you run the regex parser it’s not guaranteed that the numbers that identify the DFA states will remain the same.

I won’t continue debugging because it would consume a lot of space in this blog post.

I think that with the above explanation it’s easy to get the point.

In short we’ll repeat the above steps for each unmarked state that hasn’t been checked yet working with it against each input symbol.

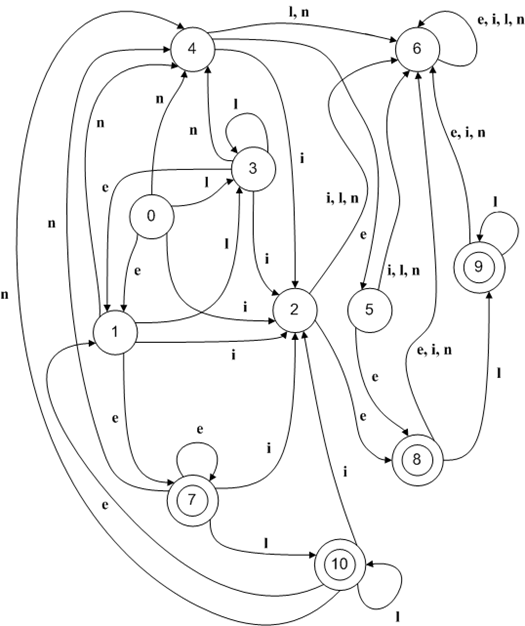
For the regex (l|e)*n?(i|e)el* in one of the times I ran the code, I got the following DFA’s transition table:

DFA start state: 0 DFA final state(s): 7 8 9 10

Trans[0, e] = 1

Trans[0, i] = 2

Trans[0, l] = 3

Trans[0, n] = 4

Trans[1, e] = 7

Trans[1, i] = 2

Trans[1, l] = 3

Trans[1, n] = 4

Trans[2, e] = 8

Trans[2, i] = 6

Trans[2, l] = 6

Trans[2, n] = 6

Trans[3, e] = 1

Trans[3, i] = 2

Trans[3, l] = 3

Trans[3, n] = 4

Trans[4, e] = 5

Trans[4, i] = 2

Trans[4, l] = 6

Trans[4, n] = 6

Trans[5, e] = 8

Trans[5, i] = 6

Trans[5, l] = 6

Trans[5, n] = 6

Trans[6, e] = 6

Trans[6, i] = 6

Trans[6, l] = 6

Trans[6, n] = 6

Trans[7, e] = 7

Trans[7, i] = 2

Trans[7, l] = 10

Trans[7, n] = 4

Trans[8, e] = 6

Trans[8, i] = 6

Trans[8, l] = 9

Trans[8, n] = 6

Trans[9, e] = 6

Trans[9, i] = 6

Trans[9, l] = 9

Trans[9, n] = 6

Trans[10, e] = 1

Trans[10, i] = 2

Trans[10, l] = 10

Trans[10, n] = 4

Figure 6 - DFA’s transition table for the regex (l|e)*n?(i|e)el*

Below is the DFA’s graph representation:

Figure 7 - DFA’s graph representation for the regex (l|e)*n?(i|e)el*

In the next post I’ll simulate some input strings against this DFA to assert its validity.

See you there!

Updated on 5/12/2009 09:57:00 PM

As I finished writing the posts, here goes the list that points to them:

Regular Expression Engine in C# (the Story)
Regex engine in C# - the Regex Parser
Regex engine in C# - the NFA
Regex engine in C# - matching strings

Source code: https://github.com/leniel/RegexEngine

I really like to study theory of computation. This series of posts show how much I like it! :)

Following the open post titled Regular Expression Engine in C# (the Story), let’s begin this endeavor with the definition of the words most used from now on:

State
A state is a unique configuration of information in a program or machine.

Finite State Machine (FSM)
A finite state machine is a model of behavior composed of a finite number of states, transitions between those states, and actions. It’s an abstract model of a machine with a primitive internal memory.

Nondeterministic Finite Automaton (NFA)
A nondeterministic finite automaton is a finite state machine where for each pair of state and input symbol there may be several possible next states.

Its mathematical model is as follow:
1. A set of states (S)
2. A set of input symbols - the input symbol alphabet (Σ)
3. A transition function that maps state-symbol pairs to a given state T : S × Σ → P(S)
4. A state s0 that is the start state s₀ ∈ S
5. A set of states that are the final states F ⊆ S

The following example explains a NFA M, with a 2 letters alphabet.

Let M = (Q, Σ, T, s₀, F) where:

• Σ = { a, b }
• Q = { s₀, s₁, s₂, s₃, s₄, s₅, s₆, s₇ }
• E({ s₀ }) = { s₀, s₁, s₄ }
• F = { s₇ }
• The transition function T can be defined by this state transition table:

State	a	b	ε
s0	{}	{}	{s1, s4}
s1	{s2}	{}	{}
s2	{s2, s3}	{s2}	{}
s3	{}	{}	{s7}
s4	{}	{s5}	{}
s5	{s5}	{s5, s6}	{}
s6	{}	{}	{s7}
s7	{}	{}	{}

Figure 1 - NFA example with 8 states

Deterministic Finite Automaton (DFA)
A deterministic finite automaton is a finite state machine where for each pair of state and input symbol there is one and only one transition to a next state.

Its mathematical model is as follow:
1. A finite set of states (S)
2. A finite set called the alphabet (Σ)
3. A transition function (δ : S × Σ → S)
4. A start state (s0 ∈ S)
5. A set of accept final states (F ⊆ S)
6. No state has an eps-transition – eps or epsilon (ε) represents "nothing" or "no input".
7. For each state S and input x, there is at most one edge labeled x leaving S.

Figure 2 - DFA equivalent to the NFA shown in Figure 1

DFA versus NFA
Despite the fact that the DFA and NFA have distinct definitions, it may be shown in the formal theory that they are equivalent, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction.

Both types of automata recognize only regular languages.

DFA + NFA = FSM

Regular Expression (regex)
A regular expression provide a concise and flexible means for identifying strings of text of interest, such as particular characters, words, or patterns of characters. Regular expressions are written in a formal language that can be interpreted by a regular expression processor (engine), a program that either serves as a parser generator or examines text and identifies parts that match the provided pattern (regex).

A regex (any regex!) can be represented as a FSM.

Some symbols you’ll encounter in regexes and their meanings:

Alternation

A vertical bar separates alternatives. For example, gray|grey can match "gray" or "grey".

Grouping

Parentheses are used to define the scope and precedence of the operators (among other uses). For example, gray|grey and gr(a|e)y are equivalent patterns which both describe the set of "gray" and "grey".

Quantification

A quantifier after a token (such as a character) or group specifies how often that preceding element is allowed to occur. The most common quantifiers are the question mark ?, the asterisk * and the plus sign +.

? = zero or one of the preceding element.
Example: colou?r matches both "color" and "colour".

* = zero or more of the preceding element.
Example: ab*c matches "ac", "abc", "abbc", "abbbc", and so on.

+ = one or more of the preceding element.
Example: ab+c matches "abc", "abbc", "abbbc", and so on, but not "ac".

After reading this we should be able to answer the following question:

What is the regular expression that describes the machine M shown in Figure 1 above?

The language of M can be described by the regular language given by this regular expression: ( a (a | b)* a ) | ( b (a | b)* b )

* Thanks to our fellow developer (dev) for pointing out the right regex! (see his comment bellow).

The Regex Parser
Let me show you some code.

As I’ve written in Regular Expression Engine in C# (the Story), I’ll present the code in a top-down approach, that is, from the higher level class to its dependencies.

The RegexParser class:

//
//    Regular Expression Engine C# Sample Application
//    2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
//  UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//  
//  This program sample was developed and turned in as a term paper for Lab. of
//  Compilers Construction. It was based on the source code provided by Eli Bendersky
//  [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//

using System;
using System.Text;

namespace RegularExpressionEngine
{
  /// <summary>
  /// Implements a parser for a given regular expression.
  /// </summary>
  class RegexParser
  {
    private string data;
    private int next;

    /// <summary>
    /// 
    /// </summary>
    /// <param name="data"></param>
    private void Init(string data)
    {
      this.data = Preprocess(data);
      next = 0;
    }

    /// <summary>
    /// 
    /// </summary>
    /// <returns></returns>
    private char Peek()
    {
      return (next < data.Length) ? data[next] : '\0';
    }

    /// <summary>
    /// 
    /// </summary>
    /// <returns></returns>
    private char Pop()
    {
      char cur = Peek();

      if(next < data.Length)
        ++next;

      return cur;
    }

    /// <summary>
    /// 
    /// </summary>
    /// <returns></returns>
    private int GetPos()
    {
      return next;
    }

    /// <summary>
    /// Generates concatenation chars ('.') where appropriate.
    /// </summary>
    /// <param name="in"></param>
    /// <returns></returns>
    private string Preprocess(string @in)
    {
      StringBuilder @out = new StringBuilder();

      CharEnumerator c, up;
      c = @in.GetEnumerator();
      up = @in.GetEnumerator();

      up.MoveNext();

      // In this loop c is the current char of in, up is the next one.
      while(up.MoveNext())
      {
        c.MoveNext();

        @out.Append(c.Current);

        if((char.IsLetterOrDigit(c.Current) || c.Current == ')' || c.Current == '*' ||
          c.Current == '?') && (up.Current != ')' && up.Current != '|' &&
          up.Current != '*' && up.Current != '?'))
          @out.Append('.');
      }

      // Don't forget the last char...
      if(c.MoveNext())
        @out.Append(c.Current);

      return @out.ToString();
    }

    /// <summary>
    /// 
    /// </summary>
    /// <param name="node"></param>
    /// <param name="offset"></param>
    private static void PrintTree(ParseTree node, int offset)
    {
      if(node == null)
        return;

      for(int i = 0; i < offset; ++i)
        Console.Write(" ");

      switch(node.type)
      {
        case ParseTree.NodeType.Chr:
          Console.WriteLine(node.data);
          break;
        case ParseTree.NodeType.Alter:
          Console.WriteLine("|");
          break;
        case ParseTree.NodeType.Concat:
          Console.WriteLine(".");
          break;
        case ParseTree.NodeType.Question:
          Console.WriteLine("?");
          break;
        case ParseTree.NodeType.Star:
          Console.WriteLine("*");
          break;
      }

      Console.Write("");

      PrintTree(node.left, offset + 8);
      PrintTree(node.right, offset + 8);
    }

    /// <summary>
    /// RD parser
    /// char ::= alphanumeric character (letter or digit)
    /// </summary>
    /// <returns></returns>
    private ParseTree Chr()
    {
      char data = Peek();

      if(char.IsLetterOrDigit(data) || data == '\0')
      {
        return new ParseTree(ParseTree.NodeType.Chr, this.Pop(), null, null);
      }
      else
      {
        Console.WriteLine("Parse error: expected alphanumeric, got {0} at #{1}",
        Peek(), GetPos());

        Console.ReadKey();

        Environment.Exit(1);

        return null;
      }
    }

    /// <summary>
    /// atom ::= char | '(' expr ')'
    /// </summary>
    /// <returns></returns>
    private ParseTree Atom()
    {
      ParseTree atomNode;

      if(Peek() == '(')
      {
        Pop();

        atomNode = Expr();

        if(Pop() != ')')
        {
          Console.WriteLine("Parse error: expected ')'");

          Environment.Exit(1);
        }
      }
      else
        atomNode = Chr();

      return atomNode;
    }

    /// <summary>
    /// rep ::= atom '*' | atom '?' | atom
    /// </summary>
    /// <returns></returns>
    private ParseTree Rep()
    {
      ParseTree atomNode = Atom();

      if(Peek() == '*')
      {
        Pop();

        ParseTree repNode = new ParseTree(ParseTree.NodeType.Star, null, atomNode, null);

        return repNode;
      }
      else if(Peek() == '?')
      {
        Pop();

        ParseTree repNode = new ParseTree(ParseTree.NodeType.Question, ' ', atomNode, null);

        return repNode;
      }
      else
        return atomNode;
    }

    /// <summary>
    /// concat ::= rep . concat | rep
    /// </summary>
    /// <returns></returns>
    private ParseTree Concat()
    {
      ParseTree left = Rep();

      if(Peek() == '.')
      {
        Pop();

        ParseTree right = Concat();

        ParseTree concatNode = new ParseTree(ParseTree.NodeType.Concat, null, left, right);

        return concatNode;
      }
      else
        return left;
    }

    /// <summary>
    /// expr   ::= concat '|' expr | concat
    /// </summary>
    /// <returns></returns>
    private ParseTree Expr()
    {
      ParseTree left = Concat();

      if(Peek() == '|')
      {
        Pop();

        ParseTree right = Expr();

        ParseTree exprNode = new ParseTree(ParseTree.NodeType.Alter, null, left, right);

        return exprNode;
      }
      else
        return left;
    }

    /// <summary>
    /// The main entry point of the Console Application
    /// </summary>
    /// <param name="args"></param>
    static void Main(string[] args)
    {
      if(args.Length != 3)
      {
        Console.WriteLine("Call with the regex as an argument.");

        Environment.Exit(1);
      }

      RegexParser myRegexParser = new RegexParser();

      // Passing the regex to be preprocessed.
      myRegexParser.Init(args[1]);

      // Creating a parse tree with the preprocessed regex
      ParseTree parseTree = myRegexParser.Expr();

      // Checking for a string termination character after
      // parsing the regex
      if(myRegexParser.Peek() != '\0')
      {
        Console.WriteLine("Parse error: unexpected char, got {0} at #{1}",

        myRegexParser.Peek(), myRegexParser.GetPos());

        Environment.Exit(1);
      }

      PrintTree(parseTree, 1);

      NFA nfa = NFA.TreeToNFA(parseTree);

      nfa.Show();

      DFA dfa = SubsetMachine.SubsetConstruct(nfa);

      dfa.Show();

      Console.Write("\n\n");

      Console.Write("Result: {0}", dfa.Simulate(args[2]));

      Console.ReadKey();
    }

  }
}

From the Main entry point above in the code you can see that it’s a console application that starts with 3 arguments (parameters). For example, the parameters could be:

RegularExpressionEngine "(l|e)*n?(i|e)el*" leniel

Where:

1st param = RegularExpressionEngine = name of the program (executable)

2nd param = (l|e)*n?(i|e)el* = the pattern (regex) to match (to check against)

3rd param = leniel = the input that will be tested against the regex

Next we instantiate a new RegexParser and call its Init method passing to it the second parameter - (l|e)*n?(i|e)el* - that is located at the index 1 position within the string[] args array.

At the Init method we set the variable data with the resulting string of the Preprocess() method, which as the name suggests preprocesses the regex so that we can translate it to an appropriate format to create a parse tree.

This is the preprocessed data we get for the regex: (l|e)*.n?.(i|e).e.l*

Note that it adds dots (.) where appropriate.

The regex engine presented here uses . for concatenation, | for alternation, and * for star. So, the regex (l|e)*n?(i|e)el* can be represented in a tree form, just like an arithmetic expression.

We then create a ParseTree that is nothing more than a data structure.

The ParseTree class:

using System;
using System.Text;

using input = System.Char;

namespace RegularExpressionEngine
{
  /// <summary>
  /// Parse tree
  /// </summary>
  class ParseTree
  {
    public enum NodeType
    {
      Chr,
      Star,
      Question,
      Alter,
      Concat
    }
    
    public NodeType type;
    public input? data;
    public ParseTree left;
    public ParseTree right;

    public ParseTree(NodeType type_, input? data_, ParseTree left_, ParseTree right_)
    {
      type = type_;
      data = data_;
      left = left_;
      right = right_;
    }
  }
}

The local variable parseTree is generated through the result we get from the Expr() method. This method reads the preprocessed regex to create a parse tree that will be used further to create an NFA.

If you look at the ParseTree class you’ll se that it has four properties: a nodeType, the input symbol (a character) and a left and right ParseTree. It’s a parse tree made of parse trees if you get the point.

The property nodeType stores the type of the node that can be one of four types represented by the enum NodeType.

The parse tree is created in four methods that also return a ParseTree. These methods are: Atom(), Chr(), Concat(), and Rep().

The order in which the afore mentioned methods are called is the following:

Expr() calls Concat() that calls Rep() that calls Atom(). Note that Atom() can call Expr() again in case the first character of the regex be a grouping symbol “(“.

These are the rules we must abide to create our parse tree:

expr   -> concat '|' expr | concat
concat -> rep . concat | rep
rep    -> atom '*' | atom '?' | atom
atom   -> char | '(' expr ')'
char   -> alphanumeric character (letter or digit)

/// <summary>
/// expr   ::= concat '|' expr | concat
/// </summary>
/// <returns></returns>
private ParseTree Expr()
{
  ParseTree left = Concat();

  if(Peek() == '|')
  {
    Pop();

    ParseTree right = Expr();

    ParseTree exprNode = new ParseTree(ParseTree.NodeType.Alter, null, left, right);

    return exprNode;
  }
  else
    return left;
}

We call the method Concat() within Expr():

/// <summary>
/// concat ::= rep . concat | rep
/// </summary>
/// <returns></returns>
private ParseTree Concat()
{
  ParseTree left = Rep();

  if(Peek() == '.')
  {
    Pop();

    ParseTree right = Concat();

    ParseTree concatNode = new ParseTree(ParseTree.NodeType.Concat, null, left, right);
    
    return concatNode;
  }
  else
    return left;
}

Then we call Rep() within Concat():

/// <summary>
/// rep ::= atom '*' | atom '?' | atom
/// </summary>
/// <returns></returns>
private ParseTree Rep()
{
  ParseTree atomNode = Atom();

  if(Peek() == '*')
  {
    Pop();

    ParseTree repNode = new ParseTree(ParseTree.NodeType.Star, null, atomNode, null);

    return repNode;
  }
  else if(Peek() == '?')
  {
    Pop();

    ParseTree repNode = new ParseTree(ParseTree.NodeType.Question, ' ', atomNode, null);

    return repNode;
  }
  else
    return atomNode;
}

The Atom() method is called within Rep():

/// <summary>
/// atom ::= chr | '(' expr ')'
/// </summary>
/// <returns></returns>
private ParseTree Atom()
{
  ParseTree atomNode;

  if(Peek() == '(')
  {
    Pop();

    atomNode = Expr();

    if(Pop() != ')')
    {
      Console.WriteLine("Parse error: expected ')'");

      Environment.Exit(1);
    }
  }
  else
    atomNode = Chr();

  return atomNode;
}

An interesting thing to note is that we’re using recursive calls in two methods: Expr() and Concat(). A method is recursive if it calls itself.

In Concat() we use the Peek() method to verify if the first character of the regex is an open round bracket ‘(‘. Peek() doesn’t increment the counter variable next used to access a symbol located at the index appointed by next within the data variable (the preprocessed regex). It only returns the symbol (a char).

If the first character is an ‘(‘, then we use the Pop() method to get the next character to be checked and increment the counter variable next.

As you can see in the Atom() method, we call the Expr() method again, which will then iterate all over, that is, build the tree downward.

In case the parser doesn’t find a group character ‘(‘ we fall within the else statement and then the atomNode which is itself a parse tree will receive a ParseTree object that contains a symbol.

/// <summary>
/// RD parser
/// char ::= alphanumeric character
/// </summary>
/// <returns></returns>
private ParseTree Chr()
{
  char data = Peek();

  if(char.IsLetterOrDigit(data) || data == '\0')
  {
    return new ParseTree(ParseTree.NodeType.Chr, this.Pop(), null, null);
  }
  else
  {
    Console.WriteLine("Parse error: expected alphanumeric, got {0} at #{1}",
    Peek(), GetPos());

    Environment.Exit(1);

    return null;
  }
}

We check to see if the character peeked is a letter or digit or a character that signalizes the end of a string ‘\0’. In case it is we return a new object of type ParseTree, passing to its constructor the type of the node and the symbol it’ll store. We pass null to the last two parameters because in the case of an alphanumeric (letter or digit) the node created will be a leaf node. For more on this, read the article about parse trees.

This is the parse tree we get if we execute the program with the regex
(l|e)*n?(i|e)el*:

.
        *
                |
                        l
                        e
        .
                ?
                        n
                .
                        |
                                i
                                e
                        .
                                e
                                *
                                        l

In the next post we’ll generate a NFA with this tree. I’ll then present the NFA class.

Updated on 5/12/2009 09:50:00 PM

As I finished writing the series of posts, here goes the list that points to them:

Regular Expression Engine in C# (the Story)
Regex engine in C# - the NFA
Regex engine in C# - the DFA
Regex engine in C# - matching strings

Source code: https://github.com/leniel/RegexEngine

References
[1] Bendersky, Eli. Algorithmic Forays - Part 1. March 7, 2004. Available at <http://www.gamedev.net/reference/programming/features/af1>. Accessed on February 24, 2008.

[2] Bendersky, Eli. Algorithmic Forays - Part 2. March 29, 2004. Available at <http://www.gamedev.net/reference/programming/features/af2>. Accessed on February 24, 2008.

[3] Bendersky, Eli. Algorithmic Forays - Part 3. April 28, 2004. Available at <http://www.gamedev.net/reference/programming/features/af3>. Accessed on February 24, 2008.

[4] Bendersky, Eli. Algorithmic Forays - Part 4. June 7, 2004. Available at <http://www.gamedev.net/reference/programming/features/af4>. Accessed on February 24, 2008.

[5] Bendersky, Eli. Algorithmic Forays - Part 5. August 17, 2004. Available at <http://www.gamedev.net/reference/programming/features/af5>. Accessed on February 24, 2008.

[6] Bendersky, Eli. Algorithmic Forays - Part 6. November 4, 2004. Available at <http://www.gamedev.net/reference/programming/features/af6>. Accessed on February 24, 2008.

A “long time ago”, more precisely 3 years ago, I was studying Automata and Formal Languages which was a Computer Engineering discipline in the 6th semester out of 10 at UBM.

At that time I was amazed by the new things I was learning such as NFA - Nondetermistic Finite Automaton, DFA - Deterministic Finite Automaton, Finite State Machine and Regular Expressions. For more on this, read my last post: Fortran Numerical Constants Recognizer.

For the sake of my development I started searching for programming related material that could put me informed about such amazing computer science constructs.

I then came across a series of articles at GameDev.net called Algorithmic Forays. It’s been written by Eli Bendersky. This guy did a great job putting together the base for a Regular Expression Engine that exercise the concepts of NFA and DFA. His code was presented in C++ and I took the time to learn a bit more about this powerful language too.

After reading Algorithmic Forays from part 1 through part 6 I started thinking about translating the code from C++ to C#. That’d be a great opportunity to grasp new C# constructs and at the same time get in touch with material related to the discipline afore mentioned.

Setting that in my mind I put my hands at work and after struggling here and there I got the code translated. I also thought about writing a Portuguese version of the article to be publicized at my university’s scientific magazine. The idea was to write an adapted version of the article presenting both code (C++ and C#) showing how to achieve the same results using different programming languages data structures.

I’ve sent a message to Eli asking him permission to write a Portuguese version of the article. You can read the e-mail I’ve sent Eli and his reply below:

Leniel Macaferi <le@…>

---

Algorithmic Forays for a Regex Parser

---

le@... <le@...>                                                              Wed, Jan 3, 2007 at 5:43 AM

To: eli…@…

Cc: Wellington Magalhães Leite <wml@…>

Dear Eli,

My name is Leniel and I'm a student of Computer Engineering here in
Brazil. I'm currently in the 9th term out of 10.
You can see my basic profile at
http://www.codeproject.com/script/profile/whos_who.asp?id=1224713

Today I'm on my vacation and I'm going to come back studying on February.

I'm passionate for anything related to technology and specially
programming which is my hobby just like yours.

Firstly I'd like to congratulate you by your advanced knowledge of
such great topics about Computer Science and Computer Engineering like
the one you discussed in the article Algorithmic Forays - Part 1 to 6.

Well, I've read your biography at http://eli.thegreenplace.net/about/
and I'm currently seeing your photo album. You're a great example for
us to follow due your characteristics as liking to study and liking to
travel the whole world. It's just what I want to do too as a
professional and as a traveler! You really do very well on this.

Your site is all of good! Think about the entire internet filled with
sites just like yours. With a complete bunch of interesting
information! My God it's a dream.

Coming to the real reason I'm writing to you - it's about a project
that has been proposed to me and a friend of mine called Wellington.
When we were in the 7th term at the university during our class of
Laboratory of Compiler Construction studying Lex and Yacc, our teacher
asked us to prepare an article about the process of creation of an
engine to parse Regular Expressions. Since that moment we started
searching the Internet for something that we could use as a base for
our article. For our lucky, we found your article Algorithmic Forays
at www.gamedev.net that is amazing for everyone to understand. It's
simple and direct with implementation examples.
During the 6th term at the university we had a discipline called
Automatons and Formal Languages. Was at this period that we learned
topics regarding Finite State Machines (FSM), Deterministic Finite
Automatons (DFA), Nondeterministic Finite Automatons (NFA) and Regular
Expressions. So, from there we know that a DFA + NFA = FSM! We've also
implemented some code for covering and getting a better understanding
of how such topics work in reality.

In true, we started our project preparing an article on April, May of
2006, when I particularly started converting all your Algorithmic
Foray's C++ code to the C# language that is the one I most like to use
for writing any kind of code. But due our other tasks, in other words,
other disciplines, we stopped working on this project. It's important
to mention that I could finalize translating your C++ code to C# on
the middle of May 2006.

I've learned such great things working with the code as mastering my
knowledge with the Generics in C#. I even got one third party DLL
called C5.dll from http://www.itu.dk/research/c5/ which includes lots
of new classes to work with sets of data as is necessary when dealing
with regular expressions.

Yesterday, 1/2, when I woke up I just thought why not to continue
working on that project about a regex parser. So, I started again with
new motivations.

I started translating your whole article from English to Portuguese
and I'd like to ask you if we could use some text and diagrams of your
article as the base of our article and we would present it with both
versions of code, C++ and C#.

Our aim is to forward it to be issued in our university's scientific
magazine and propagate to the ones interested – see
http://www.ubm.br/ubm/paginas/copep/inicial.php?pagina=apresentacao.php
(it's in Portuguese - you're learning Spanish and it's a little bit
alike. I've already publicized one article in this magazine with the
title: Development and Numeric Simulation of Algorithms for
Computational Resolution of Ordinary Differential Equations. It was a
project I developed while I was in the 4th term. The code was
developed using C++. Further, this article will be available in the
Internet through an indexing project that's been prepared by a
university here in Brazil.

We'll certainly cite the article's fonts as you can see in the
preliminary code I'm going to send you in this e-mail. Your great
initiative of publicizing the article must be preserved by any mean.
Haven't you used any other bibliography? Was it developed by just your
thoughts?

Remember that this code I'm sending you needs a review because I have
to pass through it to get it all in mind again and see if everything
is Ok. To run the code you just need to recompile it using a C#
compiler. I use the Microsoft Visual Studio 2005 Express Edition as
you mentioned in your home page here
http://eli.thegreenplace.net/2006/12/03/a-complete-c-development-environment-from-microsoft-free/
The initial parameter I'm using is set in the command line argument
inside the project's properties in Debug and is as follow:
RegularExpressionEngine "(a|b)*abb" aaababb
It's seems to be working Ok.
Try it for yourself!

From now on we're just waiting for your reply.

By the way, if you and your wife want to come to visit Brazil you can
certainly come to my house. I'd like to have you as my guests. Who
knows, one day I can go to Israel and meet you personally. That would
be great too. Israel is the apple of God's eye!

I simply think we have the same liking!

It was a pleasure to write to you.

My best regards,
                         Leniel Braz de Oliveira Macaferi
                         Volta Redonda, Rio de Janeiro, Brazil

---

Leniel Macaferi <le@…>

---

Algorithmic Forays for a Regex Parser

---

Eli Bendersky <eli@…>                                                Sun, Jan 21, 2007 at 2:03 AM

To: "le@…" <le@…>

Hello Leniel,

First of all, thanks for all the compliments - I'm flattered.
You can certainly use any part of the articles and the diagrams for your translation. As for my sources, I certainly didn't invent anything - I took all the material from the "Dragon Book" ("Compilers" by Aho, Sethi and Ullman), perhaps with the help of some googling, but as far as I remember, the book was the main source.

Keep being enthusiastic about your studies. That's a good thing :-)

Regards,

Eli

---

As you can see from the above e-mail, Eli agreed and so it was OK to write a Portuguese version of his articles.

As the semesters passed and new commitments queued I stopped translating the articles and I have just decided this past week that now it’s a good time to come back to it and finish the planned objective of 2 years ago.

While I write the next blog posts I’ll translate the remaining articles to Portuguese. I expect to publish it online here on this blog so that it can help people out there to learn this fascinating subject of Computation Theory.

I’ll follow a different path to explain how the regular expression engine work, that is, from part 1 to part 6 I’ll be showing each division of the engine by means of its representing class in code. I’ll do so, so that I can present each part of the translated code (C++ to C#) in such a way that it gets easier to understand. I’ll use a top down approach, that is, I’ll begin showing the higher level class and then I’ll go deep to its dependencies.

This is the story behind the Regular Expression Engine in C# I’ll be presenting in the next posts, starting with this one.

Hope that you like it as much as I do. This was for sure one of or even the best discipline I’ve had in the Computer Engineering course and one of the more exciting things to write about.

Updated on 5/12/2009 09:41:00 PM

As I finished writing the series of posts, here goes the list that points to them:

Regex engine in C# - the Regex Parser
Regex engine in C# - the NFA
Regex engine in C# - the DFA
Regex engine in C# - matching strings

Source code: https://github.com/leniel/RegexEngine