If you want to see how to use PLINQ (Parallel LINQ) to get performance gains when performing this calculation, take a look at the post titled
Parallel LINQ (PLINQ) with Visual Studio 2010.
To serve as a processing test in a follow up post I’m posting how to calculate prime numbers using a LINQ query expression.
In mathematics, a prime number (or a prime) is a natural number which has exactly two distinct natural number divisors: 1 and itself. The first twenty-five prime numbers are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
The following code[1] shows how to calculate the prime numbers that are less equal ( <= ) a given number “max”:
Func<int, IEnumerable<int>> primeNumbers = max =>
from i in Enumerable.Range(2, max - 1)
where Enumerable.Range(2, i - 2).All(j => i % j != 0)
select i;
IEnumerable<int> result = primeNumbers(10);
foreach(int i in result)
{
Console.WriteLine(i);
}
In my final computer engineering assignment I presented LINQ - Language Integrated Query and its constructs. With such constructs it’s possible to achieve a high degree of method chaining.
LINQ is declarative, not imperative. It allows us to simply state what we want to do without worrying about how it is done.
In the code above we declare a Func<(Of <(T, TResult>)>) generic delegate which has an int as input parameter and an IEnumerable<int> as the result.
Func delegates are very useful for encapsulating user-defined expressions that are applied to each element in a set of source data.
Using a lambda expression ( => ) we assign a query expression to the delegate.
A lambda expression is an anonymous function that can contain expressions and statements, and can be used to create delegates or expression tree types.
The query expression states that from each value i in the Enumerable.Range(2, max - 1) where all elements of the range Enumerable.Range(2, i – 2) satisfy the condition All(j => i % j != 0), we select i.
max is the delegate input parameter.
The % symbol is the modulus operator in C#. It computes the remainder after dividing its first operand by its second.
For example: considering max = 10 we’d have the following…
The range in the from clause is: { 2, 3, 4, 5, 6, 7, 8, 9, 10 }
Taking the 1st value out of the from range, we have i = 2.
The range in the where clause is Range (2, 2 - 2) = Range (2 , 0) = { }.
Since i = 2 is by default included in the result, what must be evaluated lies where the variable max is used. So, taking the 2nd value and assigning it to i we have i = 3.
The range in the where clause is Range (2, 3 - 2) = Range (2 , 1) = { 2 }.
Evaluating j => i % j we have 3 % 2 = 1, and so, 3 is a prime number.
Taking the 3rd value and assigning it to i we have i = 4.
The range in the where clause is Range (2, 4 - 2) = Range (2, 2) = { 2, 3 }.
Evaluating j => i % j we have 4 % 2 = 0 and 4 % 3 = 1, and so 4 is not a prime number because all elements of the where range must yield a result != 0 for the expression i % j != 0.
Now we have i = 5.
The range in the where clause is Range (2, 5 - 2) = Range (2 , 3) = { 2, 3, 4 }.
Evaluating j => i % j we have 5 % 2 = 1, 5 % 3 = 2 and 5 % 4 = 1. From this we have that 5 is a prime number.
Now we have i = 6.
The range in the where clause is Range (2, 6 - 2) = Range (2 , 4) = { 2, 3, 4, 5 }.
Evaluating j => i % j we have 6 % 2 = 0, 6 % 3 = 0, 6 % 4 = 2 and 6 % 5 = 1. From this we have that 6 is not prime number.
Now we have i = 7.
The range in the where clause is Range (2, 7 - 2) = Range (2 , 5) = { 2, 3, 4, 5, 6 }.
Evaluating j => i % j we have 7 % 2 = 1, 7 % 3 = 1, 7 % 4 = 3, 7 % 5 = 2 and 7 % 6 = 1. From this we have that 7 is prime number.
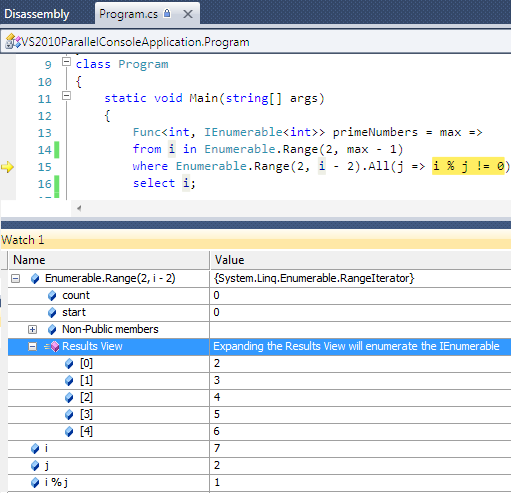
Now we have i = 8.
The range in the where clause is Range (2, 8 - 2) = Range (2 , 6) = { 2, 3, 4, 5, 6, 7 }.
Evaluating j => i % j we have 8 % 2 = 0, 8 % 3 = 2, 8 % 4 = 0, 8 % 5 = 3, 8 % 6 = 2 and 8 % 7 = 1. 8 isn’t a prime number.
Now we have i = 9.
The range in the where clause is Range (2, 9 - 2) = Range (2 , 7) = { 2, 3, 4, 5, 6, 7, 8 }.
Evaluating j => i % j we have 9 % 2 = 1, 9 % 3 = 0, 9 % 4 = 1, 9 % 5 = 4, 9 % 6 = 3, 9 % 7 = 2 and 9 % 8 = 1. 9 isn’t a prime number.
Now we have i = 10.
The range in the where clause is Range (2, 10 - 2) = Range (2 , 8) = { 2, 3, 4, 5, 6, 7, 8, 9 }.
Evaluating j => i % j we have 10 % 2 = 0, 10 % 3 = 1, 10 % 4 = 2, 10 % 5 = 0, 10 % 6 = 4, 10 % 7 = 3, 10 % 8 = 2 and 10 % 9 = 1. 10 isn’t a prime number.
Finally we have 4 prime numbers <= 10; they are: { 2, 3, 5, 7 }.
The following table illustrates the result:
| i |
where Range(2, i - 2) |
All(j => i % j != 0) |
| 2 |
{ } |
|
| 3 |
{ 2 } |
3 % 2 = 1 |
| 4 |
{ 2, 3 } |
4 % 2 = 0
4 % 3 = 1 |
| 5 |
{ 2, 3, 4 } |
5 % 2 = 1
5 % 3 = 2
5 % 4 = 1 |
| 6 |
{ 2, 3, 4, 5 } |
6 % 2 = 0
6 % 3 = 0
6 % 4 = 2
6 % 5 = 1 |
| 7 |
{ 2, 3, 4, 5, 6 } |
7 % 2 = 1
7 % 3 = 1
7 % 4 = 3
7 % 5 = 2
7 % 6 = 1 |
| 8 |
{ 2, 3, 4, 5, 6, 7 } |
8 % 2 = 0
8 % 3 = 2
8 % 4 = 0
8 % 5 = 3
8 % 6 = 2
8 % 7 = 1 |
| 9 |
{ 2, 3, 4, 5, 6, 7, 8 } |
9 % 2 = 1
9 % 3 = 0
9 % 4 = 1
9 % 5 = 4
9 % 6 = 3
9 % 7 = 2
9 % 8 = 1 |
| 10 |
{ 2, 3, 4, 5, 6, 7, 8, 9 } |
10 % 2 = 0
10 % 3 = 1
10 % 4 = 2
10 % 5 = 0
10 % 6 = 4
10 % 7 = 3
10 % 8 = 2
10 % 9 = 1 |
I’ll use the primeNumbers delegate in a future post to evaluate PLINQ (Parallel LINQ) and measure the performance gains when the same calculation is done in parallel instead of in sequence.
References
[1] Perfetti, Michel. LINQ Quiz: The list of prime numbers in 3 clauses? 2007. Available at <http://blogs.developpeur.org/raptorxp/archive/2007/11/26/quizz-linq-la-liste-des-nombres-premiers-en-3-clauses.aspx>. Accessed on May 31, 2009.

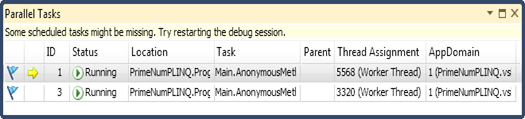
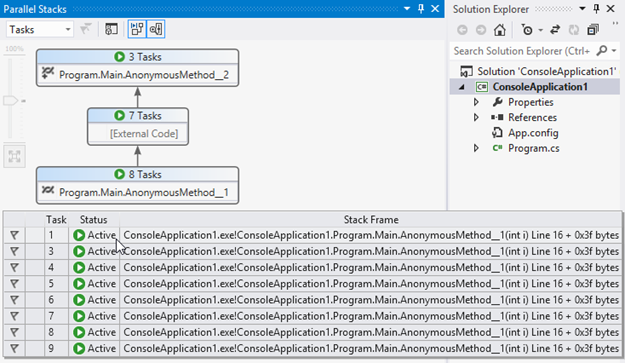 Figure 3 - The Parallel Stacks window in Visual Studio 2012 ( #8 threads )
Figure 3 - The Parallel Stacks window in Visual Studio 2012 ( #8 threads )