I really like to study theory of computation. This series of posts show how much I like it! :)
Following the open post titled Regular Expression Engine in C# (the Story), let’s begin this endeavor with the definition of the words most used from now on:
State
A state is a unique configuration of information in a program or machine.
Finite State Machine (FSM)
A finite state machine is a model of behavior composed of a finite number of states, transitions between those states, and actions. It’s an abstract model of a machine with a primitive internal memory.
Nondeterministic Finite Automaton (NFA)
A nondeterministic finite automaton is a finite state machine where for each pair of state and input symbol there may be several possible next states.
Its mathematical model is as follow:
1. A set of states (S)
2. A set of input symbols - the input symbol alphabet (Σ)
3. A transition function that maps state-symbol pairs to a given state T : S × Σ → P(S)
4. A state s0 that is the start state s0 ∈ S
5. A set of states that are the final states F ⊆ S
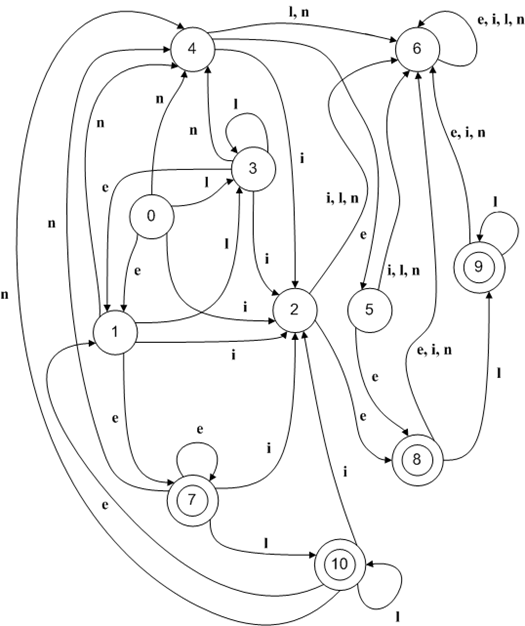
The following example explains a NFA M, with a 2 letters alphabet.
Let M = (Q, Σ, T, s0, F) where:
- Σ = { a, b }
- Q = { s0, s1, s2, s3, s4, s5, s6, s7 }
- E({ s0 }) = { s0, s1, s4 }
- F = { s7 }
- The transition function T can be defined by this state transition table:
| State | a | b | ε |
| s0 | {} | {} | {s1, s4} |
| s1 | {s2} | {} | {} |
| s2 | {s2, s3} | {s2} | {} |
| s3 | {} | {} | {s7} |
| s4 | {} | {s5} | {} |
| s5 | {s5} | {s5, s6} | {} |
| s6 | {} | {} | {s7} |
| s7 | {} | {} | {} |

Figure 1 - NFA example with 8 states
Deterministic Finite Automaton (DFA)
A deterministic finite automaton is a finite state machine where for each pair of state and input symbol there is one and only one transition to a next state.
Its mathematical model is as follow:
1. A finite set of states (S)
2. A finite set called the alphabet (Σ)
3. A transition function (δ : S × Σ → S)
4. A start state (s0 ∈ S)
5. A set of accept final states (F ⊆ S)
6. No state has an eps-transition – eps or epsilon (ε) represents "nothing" or "no input".
7. For each state S and input x, there is at most one edge labeled x leaving S.

Figure 2 - DFA equivalent to the NFA shown in Figure 1
DFA versus NFA
Despite the fact that the DFA and NFA have distinct definitions, it may be shown in the formal theory that they are equivalent, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction.
Both types of automata recognize only regular languages.
DFA + NFA = FSM
Regular Expression (regex)
A regular expression provide a concise and flexible means for identifying strings of text of interest, such as particular characters, words, or patterns of characters. Regular expressions are written in a formal language that can be interpreted by a regular expression processor (engine), a program that either serves as a parser generator or examines text and identifies parts that match the provided pattern (regex).
A regex (any regex!) can be represented as a FSM.
Some symbols you’ll encounter in regexes and their meanings:
- Alternation
- A vertical bar separates alternatives. For example,
gray|grey can match "gray" or "grey". - Grouping
- Parentheses are used to define the scope and precedence of the operators (among other uses). For example,
gray|grey and gr(a|e)y are equivalent patterns which both describe the set of "gray" and "grey". - Quantification
- A quantifier after a token (such as a character) or group specifies how often that preceding element is allowed to occur. The most common quantifiers are the question mark
?, the asterisk * and the plus sign +.
-
? = zero or one of the preceding element.
Example: colou?r matches both "color" and "colour".
* = zero or more of the preceding element.
Example: ab*c matches "ac", "abc", "abbc", "abbbc", and so on.
+ = one or more of the preceding element.
Example: ab+c matches "abc", "abbc", "abbbc", and so on, but not "ac".
After reading this we should be able to answer the following question:
What is the regular expression that describes the machine M shown in Figure 1 above?
The language of M can be described by the regular language given by this regular expression: ( a (a | b)* a ) | ( b (a | b)* b )
* Thanks to our fellow developer (dev) for pointing out the right regex! (see his comment bellow).
The Regex Parser
Let me show you some code.
As I’ve written in Regular Expression Engine in C# (the Story), I’ll present the code in a top-down approach, that is, from the higher level class to its dependencies.
The RegexParser class:
//
// Regular Expression Engine C# Sample Application
// 2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
// UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//
// This program sample was developed and turned in as a term paper for Lab. of
// Compilers Construction. It was based on the source code provided by Eli Bendersky
// [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//
using System;
using System.Text;
namespace RegularExpressionEngine
{
/// <summary>
/// Implements a parser for a given regular expression.
/// </summary>
class RegexParser
{
private string data;
private int next;
/// <summary>
///
/// </summary>
/// <param name="data"></param>
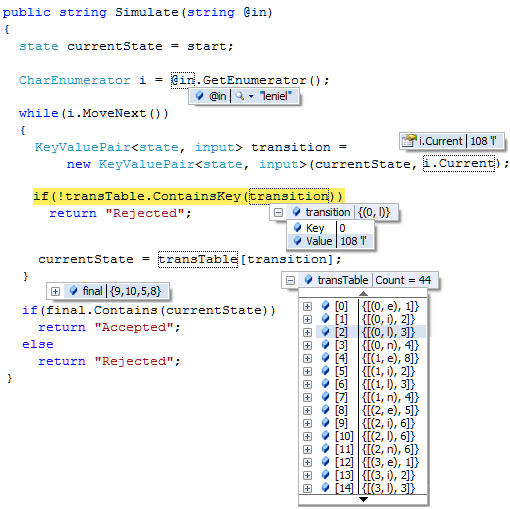
private void Init(string data)
{
this.data = Preprocess(data);
next = 0;
}
/// <summary>
///
/// </summary>
/// <returns></returns>
private char Peek()
{
return (next < data.Length) ? data[next] : '\0';
}
/// <summary>
///
/// </summary>
/// <returns></returns>
private char Pop()
{
char cur = Peek();
if(next < data.Length)
++next;
return cur;
}
/// <summary>
///
/// </summary>
/// <returns></returns>
private int GetPos()
{
return next;
}
/// <summary>
/// Generates concatenation chars ('.') where appropriate.
/// </summary>
/// <param name="in"></param>
/// <returns></returns>
private string Preprocess(string @in)
{
StringBuilder @out = new StringBuilder();
CharEnumerator c, up;
c = @in.GetEnumerator();
up = @in.GetEnumerator();
up.MoveNext();
// In this loop c is the current char of in, up is the next one.
while(up.MoveNext())
{
c.MoveNext();
@out.Append(c.Current);
if((char.IsLetterOrDigit(c.Current) || c.Current == ')' || c.Current == '*' ||
c.Current == '?') && (up.Current != ')' && up.Current != '|' &&
up.Current != '*' && up.Current != '?'))
@out.Append('.');
}
// Don't forget the last char...
if(c.MoveNext())
@out.Append(c.Current);
return @out.ToString();
}
/// <summary>
///
/// </summary>
/// <param name="node"></param>
/// <param name="offset"></param>
private static void PrintTree(ParseTree node, int offset)
{
if(node == null)
return;
for(int i = 0; i < offset; ++i)
Console.Write(" ");
switch(node.type)
{
case ParseTree.NodeType.Chr:
Console.WriteLine(node.data);
break;
case ParseTree.NodeType.Alter:
Console.WriteLine("|");
break;
case ParseTree.NodeType.Concat:
Console.WriteLine(".");
break;
case ParseTree.NodeType.Question:
Console.WriteLine("?");
break;
case ParseTree.NodeType.Star:
Console.WriteLine("*");
break;
}
Console.Write("");
PrintTree(node.left, offset + 8);
PrintTree(node.right, offset + 8);
}
/// <summary>
/// RD parser
/// char ::= alphanumeric character (letter or digit)
/// </summary>
/// <returns></returns>
private ParseTree Chr()
{
char data = Peek();
if(char.IsLetterOrDigit(data) || data == '\0')
{
return new ParseTree(ParseTree.NodeType.Chr, this.Pop(), null, null);
}
else
{
Console.WriteLine("Parse error: expected alphanumeric, got {0} at #{1}",
Peek(), GetPos());
Console.ReadKey();
Environment.Exit(1);
return null;
}
}
/// <summary>
/// atom ::= char | '(' expr ')'
/// </summary>
/// <returns></returns>
private ParseTree Atom()
{
ParseTree atomNode;
if(Peek() == '(')
{
Pop();
atomNode = Expr();
if(Pop() != ')')
{
Console.WriteLine("Parse error: expected ')'");
Environment.Exit(1);
}
}
else
atomNode = Chr();
return atomNode;
}
/// <summary>
/// rep ::= atom '*' | atom '?' | atom
/// </summary>
/// <returns></returns>
private ParseTree Rep()
{
ParseTree atomNode = Atom();
if(Peek() == '*')
{
Pop();
ParseTree repNode = new ParseTree(ParseTree.NodeType.Star, null, atomNode, null);
return repNode;
}
else if(Peek() == '?')
{
Pop();
ParseTree repNode = new ParseTree(ParseTree.NodeType.Question, ' ', atomNode, null);
return repNode;
}
else
return atomNode;
}
/// <summary>
/// concat ::= rep . concat | rep
/// </summary>
/// <returns></returns>
private ParseTree Concat()
{
ParseTree left = Rep();
if(Peek() == '.')
{
Pop();
ParseTree right = Concat();
ParseTree concatNode = new ParseTree(ParseTree.NodeType.Concat, null, left, right);
return concatNode;
}
else
return left;
}
/// <summary>
/// expr ::= concat '|' expr | concat
/// </summary>
/// <returns></returns>
private ParseTree Expr()
{
ParseTree left = Concat();
if(Peek() == '|')
{
Pop();
ParseTree right = Expr();
ParseTree exprNode = new ParseTree(ParseTree.NodeType.Alter, null, left, right);
return exprNode;
}
else
return left;
}
/// <summary>
/// The main entry point of the Console Application
/// </summary>
/// <param name="args"></param>
static void Main(string[] args)
{
if(args.Length != 3)
{
Console.WriteLine("Call with the regex as an argument.");
Environment.Exit(1);
}
RegexParser myRegexParser = new RegexParser();
// Passing the regex to be preprocessed.
myRegexParser.Init(args[1]);
// Creating a parse tree with the preprocessed regex
ParseTree parseTree = myRegexParser.Expr();
// Checking for a string termination character after
// parsing the regex
if(myRegexParser.Peek() != '\0')
{
Console.WriteLine("Parse error: unexpected char, got {0} at #{1}",
myRegexParser.Peek(), myRegexParser.GetPos());
Environment.Exit(1);
}
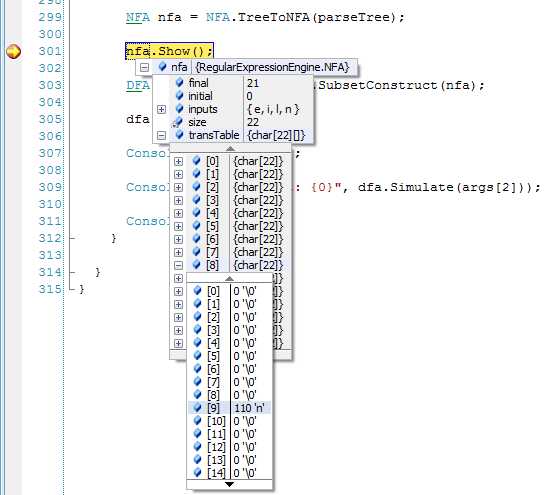
PrintTree(parseTree, 1);
NFA nfa = NFA.TreeToNFA(parseTree);
nfa.Show();
DFA dfa = SubsetMachine.SubsetConstruct(nfa);
dfa.Show();
Console.Write("\n\n");
Console.Write("Result: {0}", dfa.Simulate(args[2]));
Console.ReadKey();
}
}
}
From the Main entry point above in the code you can see that it’s a console application that starts with 3 arguments (parameters). For example, the parameters could be:
RegularExpressionEngine "(l|e)*n?(i|e)el*" leniel
Where:
1st param = RegularExpressionEngine = name of the program (executable)
2nd param = (l|e)*n?(i|e)el* = the pattern (regex) to match (to check against)
3rd param = leniel = the input that will be tested against the regex
Next we instantiate a new RegexParser and call its Init method passing to it the second parameter - (l|e)*n?(i|e)el* - that is located at the index 1 position within the string[] args array.
At the Init method we set the variable data with the resulting string of the Preprocess() method, which as the name suggests preprocesses the regex so that we can translate it to an appropriate format to create a parse tree.
This is the preprocessed data we get for the regex: (l|e)*.n?.(i|e).e.l*
Note that it adds dots (.) where appropriate.
The regex engine presented here uses . for concatenation, | for alternation, and * for star. So, the regex (l|e)*n?(i|e)el* can be represented in a tree form, just like an arithmetic expression.
We then create a ParseTree that is nothing more than a data structure.
The ParseTree class:
using System;
using System.Text;
using input = System.Char;
namespace RegularExpressionEngine
{
/// <summary>
/// Parse tree
/// </summary>
class ParseTree
{
public enum NodeType
{
Chr,
Star,
Question,
Alter,
Concat
}
public NodeType type;
public input? data;
public ParseTree left;
public ParseTree right;
public ParseTree(NodeType type_, input? data_, ParseTree left_, ParseTree right_)
{
type = type_;
data = data_;
left = left_;
right = right_;
}
}
}
The local variable parseTree is generated through the result we get from the Expr() method. This method reads the preprocessed regex to create a parse tree that will be used further to create an NFA.
If you look at the ParseTree class you’ll se that it has four properties: a nodeType, the input symbol (a character) and a left and right ParseTree. It’s a parse tree made of parse trees if you get the point.
The property nodeType stores the type of the node that can be one of four types represented by the enum NodeType.
The parse tree is created in four methods that also return a ParseTree. These methods are: Atom(), Chr(), Concat(), and Rep().
The order in which the afore mentioned methods are called is the following:
Expr() calls Concat() that calls Rep() that calls Atom(). Note that Atom() can call Expr() again in case the first character of the regex be a grouping symbol “(“.
These are the rules we must abide to create our parse tree:
expr -> concat '|' expr | concat
concat -> rep . concat | rep
rep -> atom '*' | atom '?' | atom
atom -> char | '(' expr ')'
char -> alphanumeric character (letter or digit)
/// <summary>
/// expr ::= concat '|' expr | concat
/// </summary>
/// <returns></returns>
private ParseTree Expr()
{
ParseTree left = Concat();
if(Peek() == '|')
{
Pop();
ParseTree right = Expr();
ParseTree exprNode = new ParseTree(ParseTree.NodeType.Alter, null, left, right);
return exprNode;
}
else
return left;
}
We call the method Concat() within Expr():
/// <summary>
/// concat ::= rep . concat | rep
/// </summary>
/// <returns></returns>
private ParseTree Concat()
{
ParseTree left = Rep();
if(Peek() == '.')
{
Pop();
ParseTree right = Concat();
ParseTree concatNode = new ParseTree(ParseTree.NodeType.Concat, null, left, right);
return concatNode;
}
else
return left;
}
Then we call Rep() within Concat():
/// <summary>
/// rep ::= atom '*' | atom '?' | atom
/// </summary>
/// <returns></returns>
private ParseTree Rep()
{
ParseTree atomNode = Atom();
if(Peek() == '*')
{
Pop();
ParseTree repNode = new ParseTree(ParseTree.NodeType.Star, null, atomNode, null);
return repNode;
}
else if(Peek() == '?')
{
Pop();
ParseTree repNode = new ParseTree(ParseTree.NodeType.Question, ' ', atomNode, null);
return repNode;
}
else
return atomNode;
}
The Atom() method is called within Rep():
/// <summary>
/// atom ::= chr | '(' expr ')'
/// </summary>
/// <returns></returns>
private ParseTree Atom()
{
ParseTree atomNode;
if(Peek() == '(')
{
Pop();
atomNode = Expr();
if(Pop() != ')')
{
Console.WriteLine("Parse error: expected ')'");
Environment.Exit(1);
}
}
else
atomNode = Chr();
return atomNode;
}
An interesting thing to note is that we’re using recursive calls in two methods: Expr() and Concat(). A method is recursive if it calls itself.
In Concat() we use the Peek() method to verify if the first character of the regex is an open round bracket ‘(‘. Peek() doesn’t increment the counter variable next used to access a symbol located at the index appointed by next within the data variable (the preprocessed regex). It only returns the symbol (a char).
If the first character is an ‘(‘, then we use the Pop() method to get the next character to be checked and increment the counter variable next.
As you can see in the Atom() method, we call the Expr() method again, which will then iterate all over, that is, build the tree downward.
In case the parser doesn’t find a group character ‘(‘ we fall within the else statement and then the atomNode which is itself a parse tree will receive a ParseTree object that contains a symbol.
/// <summary>
/// RD parser
/// char ::= alphanumeric character
/// </summary>
/// <returns></returns>
private ParseTree Chr()
{
char data = Peek();
if(char.IsLetterOrDigit(data) || data == '\0')
{
return new ParseTree(ParseTree.NodeType.Chr, this.Pop(), null, null);
}
else
{
Console.WriteLine("Parse error: expected alphanumeric, got {0} at #{1}",
Peek(), GetPos());
Environment.Exit(1);
return null;
}
}
We check to see if the character peeked is a letter or digit or a character that signalizes the end of a string ‘\0’. In case it is we return a new object of type ParseTree, passing to its constructor the type of the node and the symbol it’ll store. We pass null to the last two parameters because in the case of an alphanumeric (letter or digit) the node created will be a leaf node. For more on this, read the article about parse trees.
This is the parse tree we get if we execute the program with the regex
(l|e)*n?(i|e)el*:
.
*
|
l
e
.
?
n
.
|
i
e
.
e
*
l
In the next post we’ll generate a NFA with this tree. I’ll then present the NFA class.
Updated on 5/12/2009 09:50:00 PM
As I finished writing the series of posts, here goes the list that points to them:
Regular Expression Engine in C# (the Story)
Regex engine in C# - the NFA
Regex engine in C# - the DFA
Regex engine in C# - matching strings
Source code: https://github.com/leniel/RegexEngine
References
[1] Bendersky, Eli. Algorithmic Forays - Part 1. March 7, 2004. Available at <http://www.gamedev.net/reference/programming/features/af1>. Accessed on February 24, 2008.
[2] Bendersky, Eli. Algorithmic Forays - Part 2. March 29, 2004. Available at <http://www.gamedev.net/reference/programming/features/af2>. Accessed on February 24, 2008.
[3] Bendersky, Eli. Algorithmic Forays - Part 3. April 28, 2004. Available at <http://www.gamedev.net/reference/programming/features/af3>. Accessed on February 24, 2008.
[4] Bendersky, Eli. Algorithmic Forays - Part 4. June 7, 2004. Available at <http://www.gamedev.net/reference/programming/features/af4>. Accessed on February 24, 2008.
[5] Bendersky, Eli. Algorithmic Forays - Part 5. August 17, 2004. Available at <http://www.gamedev.net/reference/programming/features/af5>. Accessed on February 24, 2008.
[6] Bendersky, Eli. Algorithmic Forays - Part 6. November 4, 2004. Available at <http://www.gamedev.net/reference/programming/features/af6>. Accessed on February 24, 2008.