This time, we’ll take a look at the DFA’s class and its helper class called SubsetMachine.
To understand what’s a DFA, refer to the first post in this series called Regex engine in C# - the Regex Parser.
In the Regex engine in C# - the NFA post we ended with an NFA.
Now we’re going to build a DFA based on such NFA.
Remember that the main difference between a DFA and an NFA is that a DFA doesn’t have epsilon (ε) transitions that represent "nothing" or "no input" between states.
As described in the section DFA versus NFA in the introduction of this series of posts, it may be shown that a DFA is equivalent to an NFA, in that, for any given NFA, one may construct an equivalent DFA, and vice-versa: this is the powerset construction or subset construction.
So, let’s get our hands dirty with some code.
Below I present the DFA class:
//
// Regular Expression Engine C# Sample Application
// 2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
// UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//
// This program sample was developed and turned in as a term paper for Lab. of
// Compilers Construction. It was based on the source code provided by Eli Bendersky
// [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//
using System;
using SCG = System.Collections.Generic;
using C5;
using state = System.Int32;
using input = System.Char;
namespace RegularExpressionEngine
{
/// <summary>
/// Implements a deterministic finite automata (DFA)
/// </summary>
class DFA
{
// Start state
public state start;
// Set of final states
public Set<state> final;
// Transition table
public SCG.SortedList<KeyValuePair<state, input>, state> transTable;
public DFA()
{
final = new Set<state>();
transTable = new SCG.SortedList<KeyValuePair<state, input>, state>(new Comparer());
}
public string Simulate(string @in)
{
state curState = start;
CharEnumerator i = @in.GetEnumerator();
while(i.MoveNext())
{
KeyValuePair<state, input> transition = new KeyValuePair<state, input>(curState, i.Current);
if(!transTable.ContainsKey(transition))
return "Rejected";
curState = transTable[transition];
}
if(final.Contains(curState))
return "Accepted";
else
return "Rejected";
}
public void Show()
{
Console.Write("DFA start state: {0}\n", start);
Console.Write("DFA final state(s): ");
SCG.IEnumerator<state> iE = final.GetEnumerator();
while(iE.MoveNext())
Console.Write(iE.Current + " ");
Console.Write("\n\n");
foreach(SCG.KeyValuePair<KeyValuePair<state, input>, state> kvp in transTable)
Console.Write("Trans[{0}, {1}] = {2}\n", kvp.Key.Key, kvp.Key.Value, kvp.Value);
}
}
/// <summary>
/// Implements a comparer that suits the transTable SordedList
/// </summary>
public class Comparer : SCG.IComparer<KeyValuePair<state, input>>
{
public int Compare(KeyValuePair<state, input> transition1, KeyValuePair<state, input> transition2)
{
if(transition1.Key == transition2.Key)
return transition1.Value.CompareTo(transition2.Value);
else
return transition1.Key.CompareTo(transition2.Key);
}
}
}
As you see, a DFA has 3 variables: a start state, a set of final states and a transition table that maps transitions between states.
Below I present the SubsetMachine class that is responsible for the hard work of extracting an equivalent DFA from a given NFA:
//
// Regular Expression Engine C# Sample Application
// 2006, by Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.
//
// UBM's Computer Engineering - 7th term [http://www.ubm.br/]
//
// This program sample was developed and turned in as a term paper for Lab. of
// Compilers Construction. It was based on the source code provided by Eli Bendersky
// [http://eli.thegreenplace.net/] and is provided "as is" without warranty.
//
using System;
using SCG = System.Collections.Generic;
using C5;
using state = System.Int32;
using input = System.Char;
namespace RegularExpressionEngine
{
class SubsetMachine
{
private static int num = 0;
/// <summary>
/// Subset machine that employs the powerset construction or subset construction algorithm.
/// It creates a DFA that recognizes the same language as the given NFA.
/// </summary>
public static DFA SubsetConstruct(NFA nfa)
{
DFA dfa = new DFA();
// Sets of NFA states which is represented by some DFA state
Set<Set<state>> markedStates = new Set<Set<state>>();
Set<Set<state>> unmarkedStates = new Set<Set<state>>();
// Gives a number to each state in the DFA
HashDictionary<Set<state>, state> dfaStateNum = new HashDictionary<Set<state>, state>();
Set<state> nfaInitial = new Set<state>();
nfaInitial.Add(nfa.initial);
// Initially, EpsilonClosure(nfa.initial) is the only state in the DFAs states and it's unmarked.
Set<state> first = EpsilonClosure(nfa, nfaInitial);
unmarkedStates.Add(first);
// The initial dfa state
state dfaInitial = GenNewState();
dfaStateNum[first] = dfaInitial;
dfa.start = dfaInitial;
while(unmarkedStates.Count != 0)
{
// Takes out one unmarked state and posteriorly mark it.
Set<state> aState = unmarkedStates.Choose();
// Removes from the unmarked set.
unmarkedStates.Remove(aState);
// Inserts into the marked set.
markedStates.Add(aState);
// If this state contains the NFA's final state, add it to the DFA's set of
// final states.
if(aState.Contains(nfa.final))
dfa.final.Add(dfaStateNum[aState]);
SCG.IEnumerator<input> iE = nfa.inputs.GetEnumerator();
// For each input symbol the nfa knows...
while(iE.MoveNext())
{
// Next state
Set<state> next = EpsilonClosure(nfa, nfa.Move(aState, iE.Current));
// If we haven't examined this state before, add it to the unmarkedStates and make up a new number for it.
if(!unmarkedStates.Contains(next) && !markedStates.Contains(next))
{
unmarkedStates.Add(next);
dfaStateNum.Add(next, GenNewState());
}
KeyValuePair<state, input> transition = new KeyValuePair<state, input>();
transition.Key = dfaStateNum[aState];
transition.Value = iE.Current;
dfa.transTable[transition] = dfaStateNum[next];
}
}
return dfa;
}
/// <summary>
/// Builds the Epsilon closure of states for the given NFA
/// </summary>
/// <param name="nfa"></param>
/// <param name="states"></param>
/// <returns></returns>
static Set<state> EpsilonClosure(NFA nfa, Set<state> states)
{
// Push all states onto a stack
SCG.Stack<state> uncheckedStack = new SCG.Stack<state>(states);
// Initialize EpsilonClosure(states) to states
Set<state> epsilonClosure = states;
while(uncheckedStack.Count != 0)
{
// Pop state t, the top element, off the stack
state t = uncheckedStack.Pop();
int i = 0;
// For each state u with an edge from t to u labeled Epsilon
foreach(input input in nfa.transTable[t])
{
if(input == (char)NFA.Constants.Epsilon)
{
state u = Array.IndexOf(nfa.transTable[t], input, i);
// If u is not already in epsilonClosure, add it and push it onto stack
if(!epsilonClosure.Contains(u))
{
epsilonClosure.Add(u);
uncheckedStack.Push(u);
}
}
i = i + 1;
}
}
return epsilonClosure;
}
/// <summary>
/// Creates unique state numbers for DFA states
/// </summary>
/// <returns></returns>
private static state GenNewState()
{
return num++;
}
}
}
In the first post of this series we see the following line of code:
DFA dfa = SubsetMachine.SubsetConstruct(nfa);
The SubsetConstruct method from the SubsetMachine class receives as input an NFA and returns a DFA.
Inside the SubsetConstruct method we firstly instantiate a new DFA object and then we create two variables markedStates and unmarkedStates that are sets of NFA states which represent a DFA state.
// Sets of NFA states which is represented by some DFA state
Set<Set<state>> markedStates = new Set<Set<state>>();
Set<Set<state>> unmarkedStates = new Set<Set<state>>();
From this we see that a DFA state can represent a set of NFA states. Take a look at the introductory post and see Figure 2. It shows two DFA states that represent sets of NFA states, in this particular case the DFA final states represent the NFA states {s2, s3} and {s5, s6}.
The HashDictionary helps us to give a name (to number) each DFA state.
// Gives a number to each state in the DFA
HashDictionary<Set<state>, state> dfaStateNum = new HashDictionary<Set<state>, state>();
We declare a variable called nfaInitial that is a set of states. It receives the initial NFA state:
Set<state> nfaInitial = new Set<state>();
nfaInitial.Add(nfa.initial);
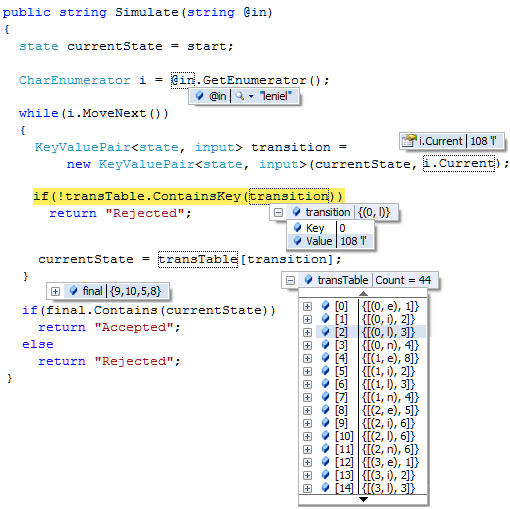
We’ll start using the EpsilonClosure function.
// Initially, EpsilonClosure(nfa.initial) is the only state in the DFAs states and it's unmarked.
Set<state> first = EpsilonClosure(nfa, nfaInitial);
The EpsilonClosure function receives as parameters the NFA and its initial state and returns a set of states. Take a look at the method signature:
static Set<state> EpsilonClosure(NFA nfa, Set<state> states)
So, what does it do? You may ask. To answer this question let’s debug this first method call:
From the NFA transition table presented in Figure 2 and from the transition graph presented in Figure 3 in the second post of this series we can see how many transitions are represented by eps transitions.
The first time we enter into this function we’ll get as a return value a set of states that contains all the states that are reachable with an eps transition from the start state 0.

Figure 1 - States reachable by an eps transition from start state 0.
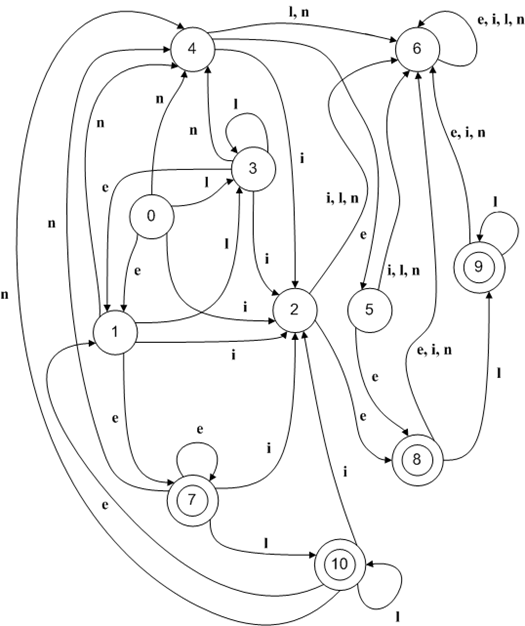
For the sake of comparison I’ll show the NFA’s graph representation for the regex (l|e)*n?(i|e)el* that we’re studying since the beginning of this series.

Figure 2 - NFA’s graph representation for the regex (l|e)*n?(i|e)el*
If you pay close attention you’ll see that the order the regex parser found the states is the order we visually debug the code looking at the graph above.
With such states found we move next adding this DFA state into the variable unmarkedStates.
We then use a function called GetNewState that is responsible for generating a number that uniquely identifies each state of the DFA:
// The initial dfa state
state dfaInitial = GenNewState();
When we pass to the next line of code we add to the dfaStateNum dictionary a key that is the set of states returned by the EpsilonClosure function and a value that is the name of the initial state of the DFA.
dfaStateNum[first] = dfaInitial;
We make the initial state of the DFA be the dfaInitial value we just got.
dfa.start = dfaInitial;
Next we enter in the first while keyword. In this while we basically extract one of the unmarkedStates and add the same to the markedStates set. This has the meaning of telling that we already checked such state.
// Takes out one unmarked state and posteriorly mark it.
Set<state> aState = unmarkedStates.Choose();
// Removes from the unmarked set.
unmarkedStates.Remove(aState);
// Inserts into the marked set.
markedStates.Add(aState);
In the next line of code (one of the most interesting parts of the whole code) we check to see if this current DFA state (remember that it is a set of states) we’re on contains the NFA final state, if it holds true, we add it to the DFA’s set of final states:
// If this state contains the NFA's final state, add it to the DFA's set of final states.
if(aState.Contains(nfa.final))
dfa.final.Add(dfaStateNum[aState]);
Now it’s time to check against the NFA’s input symbols. To accomplish this we declare an enumerator of type state that does the job of moving through each of the input symbols in the next while code block:
SCG.IEnumerator<input> iE = nfa.inputs.GetEnumerator();
// For each input symbol the nfa knows...
while(iE.MoveNext())
{ . . .
Now it’s time to create the next DFA state. We do this by declaring a new set of states and we call the EpsilonClosure function again to fill this state, but this time we pass the EpsilonClosure function a different second parameter.
// Next state
Set<state> next = EpsilonClosure(nfa, nfa.Move(aState, iE.Current));
Let’s go deeper to take a look at this second parameter.
As you see we call the function Move that is part of the NFA class. This function receives as parameters a set of states and an input symbol to be checked against. It returns a set of states.
What the move function does is: foreach state in the set of states passed as the first parameter we check each transition present in the NFA’s transition table from this state to another state with the input symbol passed as the second parameter.
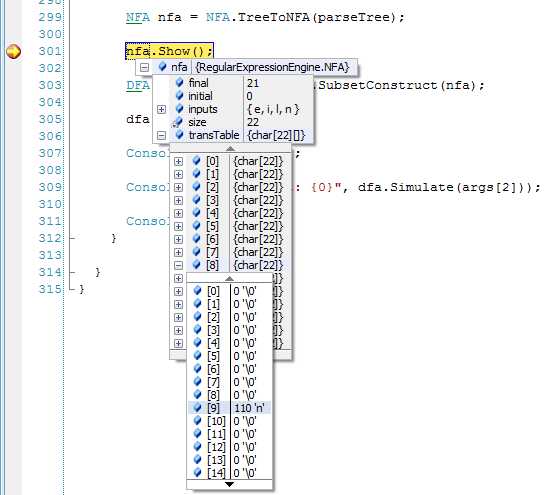
So, the first time we pass we get the following output from the Move function:

Figure 3 - Result from the NFA’s Move function the 1st time it’s called
If we look at Figure 2 we can assert that from the states present in the first state of the DFA (see Figure 1) we can move to states {5, 16} with the first NFA input that is equal to ‘e’.
With the above result taken from the Move function we’re ready to go the EpsilonClosure function for the second time to create the 2nd DFA state in the SubsetMachine class. This second time we get the following result from EpsilonClosure function:

Figure 4 - Result from the EpsilonClosure function the 2nd time it’s called
Now, if you pay close attention, we can assert that starting at the states {5, 16} we can move with an eps-transition to the states shown above. Remember that the states we pass to the EpsilonClosure function are themselves included in the result returned by the function.
Now that we have created the 2nd DFA state we check to see if it wasn’t examined yet and if it holds true we add it to the unmarkedStates variable and give a new name to this state numbering it with the GenNewState function.
// If we haven't examined this state before, add it to the unmarkedStates and make up a new number for it.
if(!unmarkedStates.Contains(next) && !markedStates.Contains(next))
{
unmarkedStates.Add(next);
dfaStateNum.Add(next, GenNewState());
}
Now the best part of it. :)
We create a new transition that has as key the number of the DFA state we’re checking and as the value the current input symbol we’re after.
KeyValuePair<state, input> transition = new KeyValuePair<state, input>();
transition.Key = dfaStateNum[aState];
transition.Value = iE.Current;
We then add this transition to the DFA’s transition table:

Figure 5 - DFA’s transition table
This has the following meaning: from state 0 with input ‘e’ go to state 1!
These are the subsequent values we get for the first unmarkedState we’re checking:
With input ‘i’ we can go to state { 14 } from which with an eps transition we can go to state { 17 }.
With input ‘l’ we can go to state { 3 } from which with an eps transition we can go to states { 4, 13, 8, 3, 12, 7, 2, 11, 6, 1, 15, 10 }.
With input ‘n’ we can go to state { 9 } from which with an eps transition we can go to states { 12, 9, 13, 15 }.
A point that deserves consideration is that each time you run the regex parser it’s not guaranteed that the numbers that identify the DFA states will remain the same.
I won’t continue debugging because it would consume a lot of space in this blog post.
I think that with the above explanation it’s easy to get the point.
In short we’ll repeat the above steps for each unmarked state that hasn’t been checked yet working with it against each input symbol.
For the regex (l|e)*n?(i|e)el* in one of the times I ran the code, I got the following DFA’s transition table:
|
DFA start state: 0
DFA final state(s): 7 8 9 10
|
| Trans[0, e] = 1 |
| Trans[0, i] = 2 |
| Trans[0, l] = 3 |
| Trans[0, n] = 4 |
| Trans[1, e] = 7 |
| Trans[1, i] = 2 |
| Trans[1, l] = 3 |
| Trans[1, n] = 4 |
| Trans[2, e] = 8 |
| Trans[2, i] = 6 |
| Trans[2, l] = 6 |
| Trans[2, n] = 6 |
| Trans[3, e] = 1 |
| Trans[3, i] = 2 |
| Trans[3, l] = 3 |
| Trans[3, n] = 4 |
| Trans[4, e] = 5 |
| Trans[4, i] = 2 |
| Trans[4, l] = 6 |
| Trans[4, n] = 6 |
| Trans[5, e] = 8 |
| Trans[5, i] = 6 |
| Trans[5, l] = 6 |
| Trans[5, n] = 6 |
| Trans[6, e] = 6 |
| Trans[6, i] = 6 |
| Trans[6, l] = 6 |
| Trans[6, n] = 6 |
| Trans[7, e] = 7 |
| Trans[7, i] = 2 |
| Trans[7, l] = 10 |
| Trans[7, n] = 4 |
| Trans[8, e] = 6 |
| Trans[8, i] = 6 |
| Trans[8, l] = 9 |
| Trans[8, n] = 6 |
| Trans[9, e] = 6 |
| Trans[9, i] = 6 |
| Trans[9, l] = 9 |
| Trans[9, n] = 6 |
| Trans[10, e] = 1 |
| Trans[10, i] = 2 |
| Trans[10, l] = 10 |
| Trans[10, n] = 4 |
Figure 6 - DFA’s transition table for the regex (l|e)*n?(i|e)el*
Below is the DFA’s graph representation:

Figure 7 - DFA’s graph representation for the regex (l|e)*n?(i|e)el*
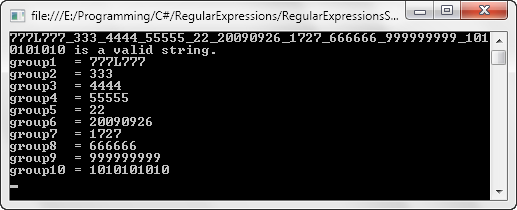
In the next post I’ll simulate some input strings against this DFA to assert its validity.
See you there!
Updated on 5/12/2009 09:57:00 PM
As I finished writing the posts, here goes the list that points to them:
Regular Expression Engine in C# (the Story)
Regex engine in C# - the Regex Parser
Regex engine in C# - the NFA
Regex engine in C# - matching strings
Source code: https://github.com/leniel/RegexEngine








 Picture 1 - Mistagged MP3 files (Title field has both the Artist and Song names)
Picture 1 - Mistagged MP3 files (Title field has both the Artist and Song names)