To close this series of posts, today I’m going to match some input strings using the regex (l|e)*n?(i|e)el* that we’ve been using since the beginning.

To match the strings I’ll make use of the DFA we constructed in the last post titled Regex engine in C# - the DFA.

These are the 20 strings I’ll be matching:

eee, eeeil, eel, ennil, ie, leie, lele, leleel, lelel, lelenil, leliel, leniel, llnel, ln, lnel, lniel, nelll, niel, nil and nll.

In the DFA class we have a method called Simulate which I show bellow:

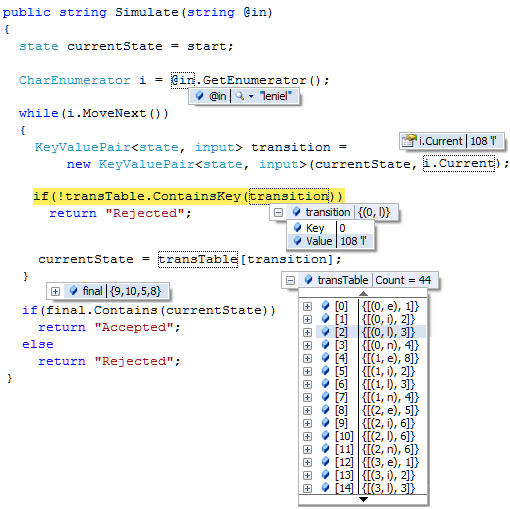
public string Simulate(string @in)
{
  state currentState = start;

  CharEnumerator i = @in.GetEnumerator();

  while(i.MoveNext())
  {
    KeyValuePair<state, input> transition = new KeyValuePair<state, input>(currentState, i.Current);

    if(!transTable.ContainsKey(transition))
      return "Rejected";

    currentState = transTable[transition];
  }

  if(final.Contains(currentState))
    return "Accepted";
  else
    return "Rejected";
}

The Simulate method takes as input a string to be matched and returns a string that signalizes success or failing when matching such a string.

To test it I’ll match the string “leniel” which by the way is my own name. :-)

So, what the Simulate method do?

It starts by assigning the start state 0 to the variable currentState.

Next we get a charEnumerator that is used in the while block to move letter by letter (input symbol by input symbol) till we get to the end of the string.

We declare a KeyValuePair<state, input> designated transition that has as the key the currentState and as the value the current input symbol we’re simulating.

We check to see if the DFA’s transition table contains such a transition, that is, if there’s a valid path from that state with that input symbol to another state. If it doesn’t, we reject the string we’re matching, otherwise we make the currentState variable receive the next state, that is, the state appointed by the transition we’ve just checked.

The process inside the while block goes on until we reach the last input symbol taken from the string we’re matching, in this case, the last “l” letter.

After getting out of the while block we make a final check to see if the state we achieved is part of the DFA’s set of final states. If it is, we accept the string, otherwise, we reject it.

This is an x-ray from the variables’ value when in the first iteration of the while block:

As you can see in the transition table, from start state (currentState) “0” with the fist input symbol “l” we can go to state “3”.

The following table shows the result obtained while testing the strings mentioned above:

Accepted	Rejected
eee	eeeil
eel	ennil
ie	lele
leie	lelel
leleel	lelenil
leliel	llnel
leniel	ln
lniel	lnel
niel	nelll
	nil
	nll

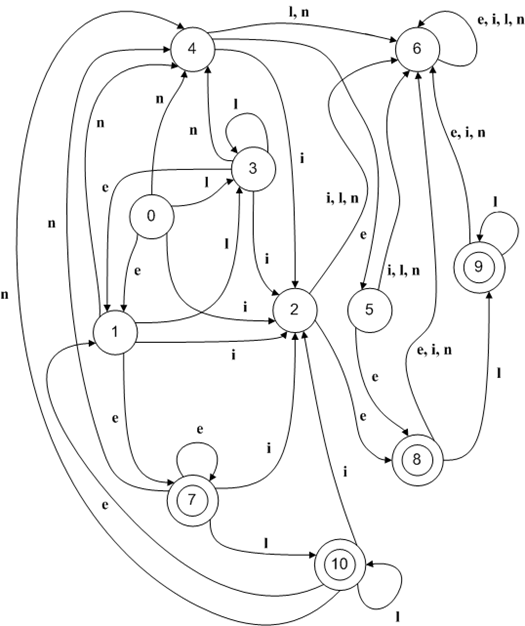
To make sure it’s correct, debug each one of these strings visually looking at the DFA’s graph representation shown below. Starting at state 0 we must end in one of the final states {7, 8, 9, 10}.

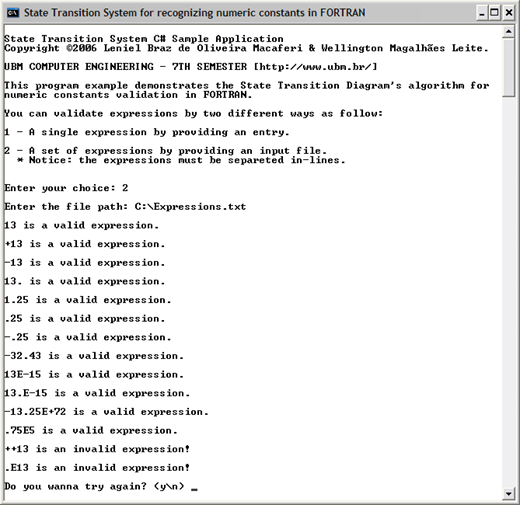
The Regex Engine executable
The Regex Engine presented in this series of posts is a C# Console Application. As such it was written in a way that its command line arguments must be entered in the following form:

RegularExpressionEngine "(l|e)*n?(i|e)el*" leniel

Where:

RegularExpressionEngine ->  the name of the executable .exe file (the program itself)

"(l|e)*n?(i|e)el*" –> between the double quotes we pass the regex

leniel –> the string we want to match in the regex

Using Microsoft Visual Studio C# 2008 we can set the command line arguments using the Debug properties page of the project like the following picture:

To get to the Debug page, right click in the solution inside Solution Explorer as shown in the following picture:

After setting the command line arguments, hit F5 and you’re ready to go.

The Regex Engine source code
You can get the complete code (Microsoft Visual C# 2008 Console application) and executable at:

http://leniel.googlepages.com/RegularExpressionEngine.rar

To try out the code you can use the free Microsoft Visual C# 2008 Express Edition that you can get at: http://www.microsoft.com/express/vcsharp

Updated on 5/12/2009 10:06:00 PM

As I finished writing the posts, here goes the list that points to them:

Regular Expression Engine in C# (the Story)
Regex engine in C# - the Regex Parser
Regex engine in C# - the NFA
Regex engine in C# - the DFA

Source code: https://github.com/leniel/RegexEngine

References
The following links can help you when dealing with regexes:

Regular-Expressions.info - Regex Tutorial, Examples and Reference - Regex Patterns
http://www.regular-expressions.info

Regular Expression Library (great site with lots of regexes and an excellent regex tester)
http://regexlib.com/Default.aspx
http://regexlib.com/RETester.aspx

Compilers construction paper
I and a dear brother in faith of mine called Wellington Magalhães Leite wrote a paper titled: Fortran Numerical Constants Recognizer

It exercises concepts related to state transition diagram, finite state machine and automata theory.

Needless to say, compilers construction was one of the best disciplines or even the best discipline I had in the computer engineering course. I really like this kind of stuff. State machines and automata theory really rocks! Automata theory is other discipline I had that really got my attention.

State Transition Diagram
This is the lexical state transition diagram in which our work is based:

Alphabet = {d, +, - , . , E} (d is any digit)

The arches of any vertex to an Error vertex aren’t showed but they exist.

Expressions like the following are recognized: 13, +13, -13, 13., 1.25, .25, -.25, -32.43, 13E-15, 13.E-15, -13.25E+72, .75E5, etc.

Expressions like the following aren’t recognized: ++13, .E13, etc.

The vertex with a 0 (zero) value is the initial state.

The vertexes with bold circles are the final states.

Note: It’s important to note that lexical state transition diagrams are finite automatons.

Abstract
A didactic method for the construction of a compiler front-end is the one substantiated in transition diagrams. So, its construction helps with the familiarization regarding the tasks of a compiler project.

This paper presents a Fortran numerical constants recognizer. It is developed based on a state transition diagram and its implementation follows the standards of the C# programming language.

Keywords: fortran, compiler construction, state transition diagram, C# programming language

CONTENTS
1 INTRODUCTION 6
  1.1 Objective	6
  1.2 Definition 6
2 DEVELOPMENT 7
  2.1 Mapping the constants 7
  2.2 Mapping the functions 7
  2.3 Application main entry point 10
3 APPLICATION 12
  3.1 Validating expressions 12
      3.1.1 Single expression 12
      3.1.2 Set of expressions 13
4 CONCLUSION 14
5 REFERENCES 15
6 ADDENDUM 16

Resumo
Um método muito didático para a construção do front-end de um compilador é aquele fundamentado em diagramas de transição. Logo, seu estudo ajuda na familiarização com as atividades envolvidas no projeto de um compilador.

Esse trabalho apresenta um sistema reconhecedor de constantes numéricas em Fortran. O mesmo é desenvolvido a partir de um diagrama de transição de estados e sua codificação segue os padrões e moldes da linguagem de programação C#.

Palavras-chave: fortran, construção de compiladores, diagrama de transição de estados, linguagem de programação C#

SUMÁRIO
1 Introdução 5
   1.1 Objetivo	5
   1.2 Definição 5
2 Desenvolvimento 6
   2.1 Mapeamento das constantes 6
   2.2 Mapeamento das funções 6
   2.3 Mapeamento da chamada principal 10
3 Aplicação 12
   3.1 Validação de expressões 12
       3.1.1 Uma única expressão 13
       3.1.2 Uma lista de expressões 14
4 Conclusão 15
5 Bibliografia	16
6 Anexo 17

Source code

class StateTransitionSystem
{
  public static void Main(string[] args)
  {
    Console.Title = "State Transition System for recognizing numeric constants in FORTRAN";

    Console.BackgroundColor = ConsoleColor.White;
    Console.ForegroundColor = ConsoleColor.Black;

    char ch;

    do
    {
      Console.Clear();

      // Print startup banner
      Console.Write("\nState Transition System C# Sample Application\n");
      Console.Write("Copyright ©2006 Leniel Braz de Oliveira Macaferi & Wellington Magalhães Leite.\n\n");
      Console.Write("UBM COMPUTER ENGINEERING - 7TH SEMESTER [http://www.ubm.br/]\n\n");

      // Describes program function
      Console.Write("This program example demonstrates the State Transition Diagram's algorithm for\n");
      Console.Write("numeric constants validation in FORTRAN.\n\n");

      // Describes program's options     
      Console.Write("You can validate expressions by two different ways as follow:\n\n");
      Console.Write("1 - A single expression by providing an entry.\n\n");
      Console.Write("2 - A set of expressions by providing an input file.\n");
      Console.Write("  * Notice: the expressions must be separeted in-lines.\n");

      Console.Write("\n\nEnter your choice: ");

      ch = Console.ReadKey().KeyChar;

      switch(ch)
      {
        case '1':
          {
            SingleExpression();
            break;
          }
        case '2':
          {
            SetOfExpressions();
            break;
          }
      }
    }
    while(ch == '1' || ch == '2');
  }

  /// <summary>
  /// Enumeration where each item corresponds to one state in the State Transition Diagram.
  /// </summary>
  public enum PossibleStates
  {
    s0 = 0,
    s1,
    s2,
    s3,
    s4,
    s5,
    s6,
    s7,
    error
  }

  /// <summary>
  /// Array of type PossibleStates, which contains the finalStates acceptable by the
  /// State Transition Diagram.
  /// </summary>
  public static PossibleStates[] finalStates = { PossibleStates.s2, PossibleStates.s3, PossibleStates.s6 };

  /// <summary>
  /// Verifies if the last state achieved by the machine belongs to the finalStates
  /// array.
  /// </summary>
  public static bool IsFinalState(PossibleStates currentState)
  {
    for(int i = 0; i < finalStates.Length; i++)
      if(currentState == finalStates[i])
        return true;

    return false;
  }

  /// <summary>
  /// Recognizes the current state and the character “label” being analysed, values
  /// passed as parameters. After, the function does the transition of state case some
  /// condition is satisfied, otherwise, the function will return an error flag.
  /// </summary>
  public static PossibleStates Recognizer(PossibleStates currentState, char c)
  {
    switch(currentState)
    {
      case PossibleStates.s0:
        {
          if(c == '+' || c == '-')
            return PossibleStates.s1;

          if(char.IsDigit(c))
            return PossibleStates.s2;

          if(c == '.')
            return PossibleStates.s4;

          break;
        }

      case PossibleStates.s1:
        {
          if(char.IsDigit(c))
            return PossibleStates.s2;

          if(c == '.')
            return PossibleStates.s4;

          break;
        }

      case PossibleStates.s2:
        {
          if(char.IsDigit(c))
            return PossibleStates.s2;

          if(c == '.')
            return PossibleStates.s3;

          if(c == 'E')
            return PossibleStates.s5;

          break;
        }

      case PossibleStates.s3:
        {
          if(char.IsDigit(c))
            return PossibleStates.s3;

          if(c == 'E')
            return PossibleStates.s5;

          break;
        }

      case PossibleStates.s4:
        {
          if(char.IsDigit(c))
            return PossibleStates.s3;

          break;
        }

      case PossibleStates.s5:
        {
          if(char.IsDigit(c))
            return PossibleStates.s6;

          if(c == '+' || c == '-')
            return PossibleStates.s7;

          break;
        }

      case PossibleStates.s6:
        {
          if(char.IsDigit(c))
            return PossibleStates.s6;

          break;
        }

      case PossibleStates.s7:
        {
          if(char.IsDigit(c))
            return PossibleStates.s6;

          break;
        }
    }
    return PossibleStates.error;
  }

  /// <summary>
  /// Reads an input expression, recognizes its characters, changes the states
  /// accordingly to those characters and hence validates the entry.
  /// </summary>
  public static void SingleExpression()
  {
    do
    {
      // The machine points to the initial state of the State Transition Diagram.
      PossibleStates currentState = PossibleStates.s0;

      Console.Write("\n\nEnter the expression to be evaluated: ");

      // strExpression receives the entry typed by the user.
      string strExpression = Console.ReadLine();

      /* For each string's character (label), calls the function Recognizer that
      on the other hand changes the machine state accordingly. */
      for(int i = 0; strExpression.Length > i; ++i)
        if(currentState != PossibleStates.error)
          currentState = Recognizer(currentState, strExpression[i]);
        else
          break;

      /* Calls the function IsFinalState to verify if the state where the machine
       stopped is a final state or not. */
      if(IsFinalState(currentState))
        Console.WriteLine("\n Valid expression.\n");
      else
        Console.WriteLine("\n Invalid expression!\n");

      Console.Write("Do you wanna try again? (y\\n) ");
    }
    while(Console.ReadKey().KeyChar == 'y');
  }

  /// <summary>
  /// Reads an input file, recognizes its lines, expression by expression and changes
  /// the states accordingly to each expression. In other words, validates the entire
  /// list.
  /// </summary>
  public static void SetOfExpressions()
  {
    do
    {
      Console.Write("\n\nEnter the file path: ");

      // Obtains the file name.
      string fileName = Console.ReadLine();

      // Verifies if the file exists.
      if(!File.Exists(fileName))
        Console.Write("\n File not found!\n\n");
      else
      {
        // Reads all the file's lines and stores them.
        StreamReader sReader = new StreamReader(fileName);

        string expression;

        // Evaluates each line until achieve the EOF (end of file).
        while((expression = sReader.ReadLine()) != null)
        {
          // The machine points to the initial state of the State Transition Diagram.
          PossibleStates currentState = PossibleStates.s0;

          /* For each expression's character (label), calls the function Recognizer that
          on the other hand changes the machine state accordingly. */
          for(int i = 0; expression.Length > i; ++i)
            if(currentState != PossibleStates.error)
              currentState = Recognizer(currentState, expression[i]);
            else
              break;

          /* Calls the function IsFinalState to verify if the state where the machine
           stopped for the expression is a final state or not. */
          if(IsFinalState(currentState))
            Console.WriteLine("\n{0} is a valid expression.", expression);
          else
            Console.WriteLine("\n{0} is an invalid expression!", expression);
        }
        sReader.Close();
      }
      Console.Write("\nDo you wanna try again? (y\\n) ");
    }
    while(Console.ReadKey().KeyChar == 'y');
  }
}

Screenshots
See screenshots of Fortran numerical constants recognizer in action:

You can get a PDF copy of the paper and the accompanying Fortran Numerical Constants Recognizer files in a ZIP file at:

English version
http://leniel.googlepages.com/FortranNumericalConstantsRecognizer.pdf

Portuguese version
http://leniel.googlepages.com/SisReconhecedorConstNumericasFortran.pdf

Microsoft Visual Studio C# 2008 Console Application project
http://leniel.googlepages.com/FortranNumericalConstantsRecognizer.zip

Note: The program’s source code is in a Microsoft Visual Studio C# 2008 Console Application project. If you don’t have Visual Studio, you can get a free copy of its express edition at http://www.microsoft.com/express/download.